ديناميكا حرارية
الديناميكا الحرارية |
فروع الديناميكا الحرارية |
ترموديناميكا الغلاف الجوي | ترموديناميكا بيولوجية | ترموديناميك الثقب الأسود | ترموديناميك كيميائي | ترموديناميك كلاسيكي | توازن ترموديناميكي | ترموديناميك اللاتوازن | ترموديناميك الظاهراتي | ديناميكا لونية كمية | ترموديناميكا إحصائية |
قوانين الديناميكا الحرارية |
القانون الصفري | القانون الأول | القانون الثاني | القانون الثالث معادلات ديناميكية حرارية |
العمليات الديناميكية الحرارية |
عملية متساوية الضغط | عملية متساوية الحرارة | عملية كظومة (أديباتية) | عملية متساوية الأنتالبية |
مصطلحات |
نظام دينامي حراري | حالة نظام ديناميكي | نظام مغلق | نظام مفتوح | نظام معزول | دورة حركة حرارية| دورة كارنو | دورة أوتو |دورة ديزل |دورة رانكن |تفاضل تام |
خواص ترموديناميكية للسوائل |
|
الديناميكا الحرارية أو التحريك الحراري أو الثرموديناميك (باللاتينية: Thermodynamica) هو أحد فروع الميكانيكا الإحصائية الذي يدرس خواص انتقال الشكل الحراري للطاقة وتحولاته إلى أوجه أخرى منها، مثل تحول الطاقة الحرارية إلى طاقة ميكانيكية مثلما في محرك احتراق داخلي والآلة البخارية ، أو تحول الطاقة الحرارية إلى طاقة كهربائية مثلما في محطات القوى , وتحول الطاقة الحركية إلى طاقة كهربائية كما في توليد الكهرباء من السدود والأنهار.
وقد تطورت أساسيات علم الترموديناميكا بدراسة تغيرات الحجم والضغط ودرجة الحرارة في الآلة البخارية. معظم هذه الدراسات تعتمد على فكرة أن أي نظام معزول في أي مكان من الكون يحتوي على كمية فيزيائية قابلة للقياس تسمى الطاقة الداخلية للنظام ويرمز لها بالرمز (U). وتمثل هذه الطاقة الداخلية مجموع الطاقة الكامنة والطاقة الحركية للذرات والجزيئات ضمن النظام، أي جميع الأنماط التي يمكن أن تنتقل مباشرة كالحرارة، كما تنتمي الطاقة الكيميائية (المختزنة في الروابط الكيميائية) و الطاقة النووية (الموجودة في نوى الذرات) إلى الطاقة الداخلية لنظام.
بدأت دراسات الديناميكا الحرارية مع اختراع الآلة البخارية وترتب عليها قوانين كثيرة تسري أيضا على جميع أنواع الآلات ؛ وبصفة خاصة تلك التي تحول الطاقة الحرارية إلى شغل ميكانيكي مثل جميع أنواع المحركات أو عند تحول الطاقة الحركية إلى طاقة كهربائية مثلا أو العكس.
نفرق في الترموديناميكا بين "نظام مفتوح " و"نظام مغلق " و" نظام معزول". في النظام المفتوح تعبر مواد النظام حدود النظام إلى الوسط المحيط ، بعكس النظام المغلق فلا يحدث تبادل للمادة بين النظام والوسط المحيط. وفي النظام المعزول فلا يحدث بالإضافة إلى ذلك تبادل للطاقة بين النظام المعزول والوسط المحيط ، وطبقا لقانون بقاء الطاقة يبقي مجموع الطاقات الموجودة فيه (طاقة حرارية ، وطاقة كيميائية ، وطاقة حركة ، وطاقة مغناطيسية ، و،إلخ) تبقي مجموعها ثابتا.
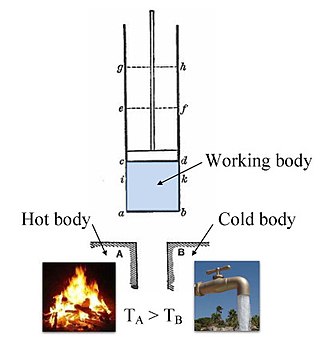
صورة ملونة للصورة الأصلية من عام 1824 لآلة كارنو تبين غلاية ساخنة ، ووسط شغال (بخار في أسطوانة ذات مكبس) ، ووسط بارد (ماء). والرموز على الاسطوانة تُعلم نقاط توقف مهمة في دورة كارنو.
توضح لنا الديناميكا الحرارية اعتماد الحرارة والشغل الميكانيكي عند حدود النظام على دوال الحالة التي تصف حالة النظام. ومن دوال الحالة التي تصف النظام نجد : درجة الحرارة T ، والضغط p ، وكثافة الجسيمات n ، والجهد الكيميائي μ وهذه تسمى "خواص مكثفة" ، وصفات أخرى مثل الطاقة الداخلية U وإنتروبيا S , والحجم V وعدد الجسيمات N ، وقد جرى العرف على تسميتها كميات شمولية. الفرق بين الكميات المكثفة والكميات الشمولية ينحصر في كون الدوال المكثفة لا تتغير بتضخيم النظام (إضافة جزء جديد) مثل الكثافة والحرارة النوعية ، أما الدوال الشمولية أو الكميات الشمولية فهي تزداد بتضخيم النظام مثل عدد الجسيمات ، والطاقة الداخلية (المحتوي الحراري في النظام).
محتويات
1 أصل الكلمة
2 تمهيد
3 التاريخ
4 تطور الديناميكا الحرارية وفروعها
4.1 ترموديناميكا كلاسيكية
4.2 ترموديناميكا إحصائية
4.3 ترموديناميكا كيميائية
5 المفاهيم الأساسية
5.1 النظام الديناميكي الحراري
5.2 كمية الحرارة
5.3 درجة الحرارة
5.4 الحرارة النوعية
5.5 السعة الحرارية
5.6 القانون الأساسي في الديناميكا الحرارية
6 قوانين الديناميكا الحرارية الأربعة
6.1 القانون الصفري للديناميكا الحرارية
6.2 القانون الأول للديناميكا الحرارية
6.3 توازن الطاقة في الدورات الحرارية
6.4 القانون الثاني للديناميكا الحرارية
6.5 القانون الثالث للديناميكا الحرارية
7 الكمونات الدينامية الحرارية
8 العمليات الدينامية الحرارية
8.1 انواع عمليات الحركة الحرارية
9 الخصائص الحرارية
9.1 المعادلة الحرارية
9.2 معادلة فان دير فالس
10 حساب الطاقة في الترموديناميكا
11 أنواع تغير الحالة
12 متغيرات مترافقة
13 اقرأ أيضا
14 مراجع
أصل الكلمة
المصطلح في اللغات الأوروبية (باللاتينية: Thermodynamica) مأخوذ من الأصول اليونانية θέρμη أي حرارة وδύναμις أي طاقة، وتترجم إلى الديناميكا الحرارية.
تمهيد

حركة الذرات والجزيئات في الغاز حركة عشوائية مهرجلة ، تتسم بإنتروبيا عالية. ملحوظة : خفضت سرعات الذرات في هذا الشكل نحو 1000.000.000.000 مرة عن طبيعتها.
في أواخر القرن الثامن عشر ظهر علم الديناميكا الحرارية كعلم يدرس تحول الطاقة الحرارية إلى عمل ميكانيكي، واستنادا إلى ذلك وضعت الأسس النظرية لعمل الآلات الحرارية. غير أن التطور المستمر في المحركات الحرارية أعطى علم الديناميكا الحرارية أهمية كبيرة تخطت حدود الهندسة الحرارية لتلقى استخداما واسعا في فروع مختلفة من العلوم الأساسية كالفيزياء والكيمياء ، وتقنية الطاقة وتقنية المحركات على اختلاف أنواعها وتقنية البطاريات . والديناميكا الحرارية الحديثة هو العلم الذي يتطرق إلى دراسة قوانين التحولات المتبادلة لمختلف أشكال الطاقة، كما ويعالج العمليات أو الظواهر التي تحدث في الطبيعة من خلال تحول الطاقة من شكل إلى آخر. وتختلف الديناميكا الحرارية عن الفيزياء والكيمياء بأنها لا تستند إلى أي نموذج لبناء المادة، كما لا ترتبط بأي تصور عن البنية الجزيئية لهذه المادة، ولكنه يعتمد على القوانين التي تم التوصل إليها تجريبيا.[1]
وعلم الديناميكا الحرارية يرتكز على ثلاث قوانين تجريبية و معادلة الحالة[1]:
القانون الأول للديناميكا الحرارية، ، أو قانون حفظ الطاقة.
القانون الثاني للديناميكا الحرارية وهو يبين اتجاه سير ظواهر طبيعية تحدث في الطبيعة ، مثل انتقال الحرارة من الجسم الساخن إلى البارد.
القانون الثالث للديناميكا الحرارية وهو يؤكد عدم بلوغ الصفر المطلق لدرجة الحرارة.
وتعطي الديناميكا الحرارية وصفا شاملا للعمليات والظواهر التي تحدث في الطبيعة بصفة عامة ، وتفسر لنا التفاعلات الكيميائية وهي هامة جدا في مجالات الصناعات الكيماوية و تكرير البترول و محطات الطاقة وإنتاج البطاريات و كفاءة المحركات وإنتاج البخار وتعيين خواص الغازات.[1]
يهتم علم الديناميكا الحرارية -كما يدل الاسم- بالحرارة أو الطاقة الحرارية بالدرجة الأولى وبكل الظواهر التي تظهر أو تتعلق بهذه الطاقة مثل عمليات انتقال الحرارة من جسم لآخر أو كيفية تخزين هذه الطاقة أو توليدها. يقوم علم الديناميكا الحرارية على أربعة قوانين كبرى وهي القانون صفر (أو القانون الرابع) والقانون الأول والقانون الثاني والقانون الثالث.
إلى جانب ذلك وهو الأهم تدرس الديناميكا الحرارية علاقة الحرارة بالتحريك الميكانيكي ، مثلما ساعدنا في ذلك على اختراع الآلة البخارية ومحرك البنزين وطرق رفع كفاءتهم ، كما تدرس الديناميكا الحرارية العلاقة بين الحرارة و تفاعل كيميائي وتطبيقاتها تجمع بين اختراع البطاريات والمركمات ، وأخيرا علاقة الحرارة بالكهرباء حيث تساعدنا على توليد الطاقة الكهربائية من عدة وسائل مثل محطات تعمل بالفحم أو بالقوى المائية أو بالطاقة النووية . كل تلك التقنيات تعتمد على تطويرها بغرض رفع كفاءتها على علم الديناميكا الحرارية .
التاريخ
قام العالم الفيزيائي الفرنسي سادي كارنو عام 1824 بدراسة كمية الحرارة التي تعمل بها آلة بخارية. وتبين له أن البخار الساخن يمكن أن يسخن ماء بارد وأن يقوم بإنتاج عمل ميكانيكي في نفس الوقت. واعتقد كارنو أنه خلال تلك العملية لا يحدث فقدا في الطاقة. كما وصف "كارنو" العمليات الجارية في الآلة البخارية بأنها عملية دورية، أي أنها دورة تتكرر مرارا. واستطاع العالم كلابيرون بعد ذلك بصياغة تلك الدورة في صياغة رياضية وسميت تلك الطريقة دورة كارنو.[2]
ثم جاء الطبيب الألماني "يوليوس ماير" عام 1841 وقدم الافتراض أن الطاقة في نظام مغلق تكون ثابتة المقدار. فلا يمكن أن تفنى الطاقة ، وإنما تتحول من صورة إلى أخرى. هذا الافتراض أصبح معروفا قانون بقاء الطاقة. وقام "ماير " بحسابات في تحويل الحرارة إلى طاقة حركة ميكانيكية. وقام بحساب كمية الطاقة اللازمة لرفع درجة حرارة 1 جرام من الماء 1 درجة مئوية ، وكم تبلغ تلك الطاقة عندما تتحول إلى طاقة ميكانيكية. وأتم ماير الحساب واتضح له أن تلك الكمية من الحرارة تكفي لرفع 1 جرام 367 متر إلى أعلى (في الحقيقة ترفعه 426 متر). وشكلت تلك الحسابات أساسا للقانون الأول للديناميكا الحرارية عن الحركة الحرارية (الترموديناميكا).[3] ثم عين جيمس جول عام 1844 المكافئ الميكانيكي الحراري بدقة كبيرة.
وفي عام 1840 قام العالم الكيميائي الألماني السويسري هيرمان هاينريش هس مقالة علمية تحت عنوان : "فحوصات حرارية كيميائية" تتعلق بظاهرة حفظ الطاقة في الجزيئات بمشاهداته الحرارة الناتجة من تفاعلات كيميائية.
وبينما كان تصور "كارنو" أن كمية الطاقة تبقى كاملة لا تتغير أثناء عمل آلة بخارية، أخذ "ماير" في الحسبان إمكانية تحول الطاقة من صورة إلى أخرى مثل تحولها إلى طاقة حركة عند تشغيل آلة . ثم جاء العالم الفيزيائي الألماني رودولف كلاوسيوس عام 1854 وربط بين الفكرتين : فكرة كارنو وفكرة ماير، وبيّن أن الآلة البخارية تعمل عندما تسري حرارة من وسط ساخن إلى وسط بارد داخل الآلة ، وأيد بذلك فكرة كارنو في أن الطاقة لا تفنى وإنما يمكن أن يتحول جزء منها إلى شغل، أي طاقة ميكانيكية (طاقة حركة). أي أن الطاقة الحرارية لا تبقى بأكملها على صورتها الحرارية - كما كان كارنو يعتقد مقدما - وإنما يتحول جزء منها إلى شغل ميكانيكي ويتسرب الباقي إلى الجو المحيط مع العادم .
واتضح ل "كلاوسيوس" أن الطاقة الحرارية في آلة (ألة بخارية) تتحول جزئيا إلى شغل ميكانيكي ، والباقي يتسرب في الجو. وتحدد الكفاءة لآلة النسبة بين الشغل الميكانيكي الناتج إلى كمية الحرارة
المزودة بها الآلة.
تلك المعلومة التي توصل إليها كلاوسيوس شكلت صيغة القانون الثاني للديناميكا الحرارية :" لا توجد آلة تعمل دوريا وينقصر عملها فقط في تحويل الحرارة (كلها) إلى شغل ميكانيكي." [4] وكمية الحرارة التي لم تنتج شغلا ميكانيكيا أثناء الدورة فهي تُعطى إلى الوسط المحيط. تلك الكمية من الحرارة (طاقة) الغير مستفاد منها ربطها كلاوسيوس بدرجة الحرارة وصاغ منها دالة جديدة أسماها إنتروبيا.
جميع العمليات التي تسير طبيعيا تحتوي على جزء من الإنتروبيا الغير عكوسية ، وظيفتها تصريف الحرارة الغير مستفاد منها إلى الوسط المحيط.
بعد ذلك صاغ بولتزمان الإنتروبيا بطريقة يسهل تصورها بأنها مقياس لعدم الانتظام (مقياس للهرجلة في نظام).
.[5] وأنه في نظام مغلق (منعزل عن الوسط المحيط) ويحدث فيه تغير عكوسي للحالة فإن فرق الإنتروبيا - بين الحالة الابتدائية والحالة النهاية - يكون مساويا للصفر.
ثم جاء العالم الكيميائي الفرنسي "مارسلين برتلوت" في عام 1862 وبين أن القوة الدافعة وراء تفاعل كيميائي تكمن في الحرارة التي تنتج من التفاعل.
وربط هيرمان هلمهولتز الألماني الطاقة الكهربائية لبطارية بالطاقة الكيميائية والطاقة الحرارية ، وتوصل في رسالته العلمية المسماة: " عن حفظ القوة " إلى قانون حفظ الطاقة، بدون علمه عن أعمال "ماير".
ثم تفرغ "هلمهولتز" خلال السنوات التالية لدراسة التفاعلات الكيميائية ، وأيد أعمال "برتولت " من حيث نشأة حرارة من تفاعلات كيميائية كثيرة ، مع أنه وجد أيضا أن بعضها يبرد أثناء التفاعل. وقام هلمهولتز في رسالته العلمية تحت عنوان :" ترموديناميكية العمليات الكيميائية" [6] بأن الطاقة تتحول خلال تفاعل كيميائي إلى طاقة حرة وطاقة داخلية ، تبقى مرتبطة بالنظام.[7] وربط "هلمهولتز" الطاقة الداخلية والطاقة الحرة بحاصل ضرب الإنتروبيا ودرجة الحرارة.
وطبقا لهلمهولتز يكون التفاعل الكيميائي ممكنا فقط عندما تنخفض الطاقة الحرارة. كذلك توصل العالم الفيزيائي الكيميائي الأمريكي ويلارد غيبس بين الأعوام 1875 - 1878 إلى نفس النتائج التي توصل إليها هلمهولتز.
وسميت العلاقة معادلة جيبس-هلمهولتز تكريما لهذاين العالمين. وبواسطتها يمكن للكيميائي معرفة إمكانية سير تفاعل وتكوين جزيئات جديدة. كما يمكنه معرفة درجة الحرارة وتركيز المواد الداخلة في التفاعل والخارجة منه.
بالإضافة إلى الترموديناميكا الكلاسيكية ابتكرت نظرية الحركة الحرارية. وطبقا لهذه النظرية يتكون الغاز من جسيمات - ذرات وجزيئات - تتحرك حرة وعشوائيا وتتصادم ببعضها البعض في فراغ بينها. وعند ارتفاع درجة الحرارة تزداد سرعة حركة الجسيمات وتكثر اصطداماتها وطذلك اصداماتها بجدار الوعاء وتمارس عليه ضغطا.
بجانب الترموديناميكا الكلاسيكية فقد تطورت نظرية الحركة الحرارية للغازات. ويتكون الغاز من جسيمات مثل الذرات أو الجزيئات تتحرك عشوائيا في فراغ وتحدث بينها اصطدامات. وعندما نرفع درجة حرارة الغاز تتحرك الجسيمات بسرعات أكبر ويزيد معدل اصطدامها بعضها البعض ، كما تمارس ضغطا على جدار الوعاء الموجودة فيه.
من العلماء الذين ساهموا في صياغة تلك النظرية رودولف كلاوسيوس، وجيمس ماكسويل، ولودفيغ بولتزمان.[8] واستخدم كل من بولتزمان وماكسويل طرق حساب الاحتمالات (الطرق الإحصائية) بغرض تفسير الكميات الترموديناميكية التي نراها ونقيسها معمليا واعتمادها على خصائص الجزيئات.
قام الفيزيائي "إليوت ليب" عام 1999 بتقديم منظومة للترموديناميكا محاولا تفسير الإنتروبيا بطريقة جديدة ، ولكن محاولته هذه لا تغير من نتائج الترموديناميكا الكلاسيكية.
ونظرا للتاريخ الطويل والمراحل العديدة التي تتطورت فيها الترموديناميكا واتساع تطبيقاتها في وصف " الحركة الحرارية التقنية " ، (مثل وصف عمل محرك الاحتراق الداخلي أو عمل الثلاجة) ، والترموديناميكا الكيميائية (مثل وصف سرعة التفاعلات الكيميائية) ،و "الترموديناميكا الإحصائية" (التي تصف مستويات الطاقة الكمومية في الجوامد) نظرا لهذا التاريخ الطويل فكل من تلك الفروع له طريقته في صياغة المعادلات.
تطور الديناميكا الحرارية وفروعها

ثمانية من العلماء ساهموا في الكشف عن الحركة الحرارية (ترموديناميك) ولهم مدارس فيها. من أهم تلك المدارس مدرسة برلين وعالمها رودولف كلاوسيوس 1865 ، ومدرسة فيينا وعالمها في الكيمياء الإحصائية لودفيج بولتزمان ، ومدرسة جامعة ييل ومؤسسها ويلارد غيبس 1876 في الترموديناميكا الكيميائية.[9]
ساهم في تطور هذا العلم رودولف كلوسيوس وويليام طمسون وهرمان فون هلمهولتز ، جوزيه غيبس ، وسادي كارنو ، وويليم رانكين وغيرهم. وقد تفرع من دراسة الأنظمة الترموديناميكية في عدة فروع ، يستخدم كل فرع منها نموذجا خاصا للمعاملة ، مثل الاعتماد على تحليل نتائج التجارب أو التحليل الرياضي ، أو تطبيق مبادئ خاصة على نظمها المختلفة. من أهم تلك الفروع نذكر :
ترموديناميكا كلاسيكية
في الترموديناميكا الكلاسيكية نقوم بوصف حالة نظام (وعلى الأخص في حالة توازنه) وعمليات الأنظمة الحركية الحرارية ("أنظمة ترموديناميكية"). ويقوم الوصف على استخدام الخواص العينية الكبيرة للنظام التي يسهل قياسها كالحرارة و الضغط و الحجم ، وكذلك وصفها بصياغة معادلات مناسبة للنتائج التجريبية. وفي هذا الإطار تقوم الترموديناميكا الكلاسيكية (أي التقليدية) بدراسة تغيرات الطاقة والشغل والحرارة وتغير المادة على أساس قوانين الديناميكا الحرارية. ويعبر التعبير "الكلاسيكية" عن أن الوصف الذي تقوم به لنظام يعتمد على متغيرات معملية يمكن قياسها بالمختبرات ، فكانت هي أول سبل تفهمنا خلال القرن التاسع عشر. ثم تبع ذلك محاولات وصف النظام الصغري (أي دراسة كياناته الصغرى) وتمثل ذلك في تطور " الترموديناميكا الإحصائية ".
ترموديناميكا إحصائية
تسمى الترموديناميكا الإحصائية أيضا " ميكانيكا إحصائية " ، وقد نشأت هذه بتقدم معرفتنا عن النظرية الذرية وتكوين الجزيئات من الذرات خلال النصف الثاني من القرن التاسع عشر ومطلع القرن العشرين. زودت تلك المعرفة الترموديناميكا بتفسيرات مبنية على التآثر بين الذرات والجزيئات ومبنية على حالات كمومية في نظام ذرات أو جزيئات وتوزيعها (إحصائيا). ويهتم هذا الفرع بالربط بين الخواص الصغرية لنظام أي في حيز الذرات والجزيئات ، وخواصه الشمولية العينية (التي يمكن مشاهدتها معمليا) . وتفسير الحركية الحرارية كنتيجة طبيعية لإحصاءات الميكانيكا التقليدية و نظرية الكم في النطاق الصغري. يعود الفضل الأكبر في تفسيرها إلى عالم الفيزياء النمساوي لودفيغ بولتزمان.
ترموديناميكا كيميائية
 مقالة مفصلة: ترمودینامیكا كيميائية
مقالة مفصلة: ترمودینامیكا كيميائية
تهتم الترموديناميكا الكيميائية (أو الحركية الحرارية الكيميائية) بدراسة العلاقة بين الطاقة والتفاعلات الكيميائية والتحول الكيميائي وكذلك بالتغيرات الفيزيائية المتعلقة بحالة نظام ترموديناميكي من وجهة قوانين الترموديناميكا. يعود الفضل الكبير في تطور فهمنا للترموديناميكا الحرارية إلى اكتشافات ويلارد غيبس 1876.
المفاهيم الأساسية
المفاهيم الأساسية في الديناميكا الحرارية هي كمية الحرارة ودرجة الحرارة والحرارة النوعية والسعة الحرارية.
وتعد مختلف أشكال الجمل الديناميكة الحرارية موضوع الدراسة الذي تتعرض له الديناميكا الحرارية.
النظام الديناميكي الحراري
 مقالة مفصلة: نظام حركة حرارية
مقالة مفصلة: نظام حركة حرارية
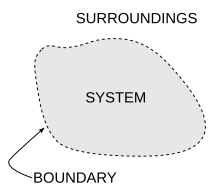
تعريف النظام والوسط المحيط والحدود بينهما.
هي جسم أو مجموعة من الأجسام المادية التي تتبادل الطاقة والمادة فيما بينها ، أو مع الوسط المحيط بها (الأجسام الواقعة خارج حدود النظام الدينامي الحراري ، والمسماة بالوسط المحيط أو الوسط الخارجي).
مثال: الغاز المحصور في أسطوانة والمكبس يشكل نظاما ديناميكيا حراريا ، حيث يمثل الهواء الجوي المحيط بالاسطوانة من الخارج "الوسط المحيط " ، وتشكل جدران الاسطوانة مع سطح المكبس حدود النظام ويشكل الغاز المحصور "الجسم العامل".
وتصنف الأنظمة الدينامية الحرارية (بعض البلاد العربية تستخدم تعبير " جملة" بدلا عن "نظام ") حسب شروط التبادل للطاقة والمادة مع الوسط الخارجي إلى مايلي[1]:
- الجملة الدينامية الحرارية المعزولة: وهي النظام الذي لا يتم تبادل لا للطاقة ولا للمادة مع الوسط المحيط.
- الجملة الدينامية الحرارية المغلقة: وهي النظام الذي لا يحدث تبادل للمادة بينه وبين الوسط المحيط ولكن يحدث بينهما تبادل للطاقة.
- الجملة الدينامية الحرارية المفتوحة: وهي النظام التي يحدث بينه وبين الوسط المحيط تبادل للمادة.
ويطلق على مجموعة الخواص الفيزيائية للجملة عند ظروف العمل بالحالة الدينامية الحرارية للجملة، فهناك الحالة المتوازنة (المستقرة)، والحالة غير المتوازنة (غير المستقرة) للجملة الدينامية الحرارية. فالحالة المتوازنة (المستقرة) للجملة الدينامية الحرارية تتميز بأن عناصر الحالة للجملة لا تتغير مع مرور الزمن تحت تأثير الظروف الخارجية الثابتة للوسط المحيط، كما يطلق على حالة الجملة الدينامية الحرارية بأنها متوازنة حراريا عندما تحافظ جميع نقاط الجملة على درجة حرارة ثابتة. وتدعى حالة الجملة الدينامية الحرارية بالمستقرة إذا حافظت عناصر الحالة للجملة في جميع نقاطها على قيم ثابتة تحت تأثير القوى الخارجية ومع مرور الزمن. أما إذا تغيرت قيمة أحد عناصر الحالة تحت تأثير الشروط الخارجية ومع مرور الزمن فتدعى حينئذ الجملة الدينامية الحرارية بغير المستقرة.
كمية الحرارة
 مقالة مفصلة: طاقة حرارية
مقالة مفصلة: طاقة حرارية
الحرارة هي إحدى صور الطاقة وتنتقل من نقطة لأخرى أو من جسم لآخر نتيجة للاختلاف في درجة حرارة الجسمين، وتقاس كمية الحرارة بوحدة الطاقة وهي الجول.
إذا قمنا بتسخين 1 كيلوجرام من الماء من درجة حرارة 15 درجة مئوية إلى 20 درجة مئوية ، يكتسب الماء كمية من الحرارة تساوي :
- كمية الحرارة المكتسبة = الحرارة النوعية للماء. 5 درجات حرارة =
- = 4810 جول/درجة مئوية. 5 درجة مئوية
- = 24050 جول
هذه هي كمية الحرارة التي يكتسبها 1 كيلوجرام ماء عند تسخينه ورفع درجة حرارته 5 درجات.
وهذا المثال يوضح أيضا الفرق بين الحرارة التي هي طاقة حرارية وتقاس بالجول ، وبين درجة الحرارة التي قد نقيسها "بدرجة سيلزيوس" أو كلفن.
يمكن تحويل الحرارة (الطاقة الحرارية) إلى أنواع أخرى من الطاقة مثل طاقة كهربائية ويتم ذلك في محطات القوى ، أو تحويل الحرارة إلى طاقة حركية مثل عمل آلة بخارية أو محرك احتراق داخلي وغيرها.
درجة الحرارة
 مقالة مفصلة: درجة حرارة
مقالة مفصلة: درجة حرارة
درجة الحرارة هي مقياس الاتزان الحراري ونعني بهذا الحالة التي عندها لا تنتقل الحرارة من نقطة لأخرى وذلك لعدم وجود فارق في درجات الحرارة. وتقاس الحرارة بوحدات مئوية أو فهرنهتية أو مطلقة. وتقاس درجات الحرارة بأنواع مختلفة من مقاييس الحرارة أهمها مقياس الحرارة السائلي، ومقياس الحرارة الغازي، ومقياس الحرارة البلاتيني، ومقياس الحرارة ذو المزدوجة الحرارية، وأخيراً مقياس الحرارة المسمى بالبيومتر الضوئي.
الحرارة النوعية
 مقالة مفصلة: حرارة نوعية
مقالة مفصلة: حرارة نوعية
هي كمية الحرارة اللازمة لرفع درجة حرارة 1 كيلوجرام من المادة درجة مئوية واحدة (أو مطلقة) وبذلك تكون وحدتها هي جول لكل كيلوجرام لكل درجة.
وحدة قياسها هي : جول / (كجم. ْم) أو جول / (كجم. كلفن)
(ملحوظة: طبقا للتعريف القديم كانت الحرارة النوعية لمادة هي كمية الحرارة اللازمة لرفع درجة حرارة 1 جرام من المادة درجة مئوية واحدة. فكانت وحدتها سعرة/جرام/درجة).
والجدول أدناه يبين الحرارة النوعية لبعض المواد :
| المادة | جول /(كجم. درجة مئوية واحدة) |
|---|---|
| الماء | 4180 |
| زيت الزيتون | 1971 |
| ألمنيوم | 895 |
| زجاج عادي | 832 |
| نحاس | 389 |
| فضة | 234 |
| الزئبق | 139 |
| الذهب | 125 |
وسبب اختلاف الحرارة النوعية من مادة إلى أخرى يعود إلى مدى تراص وترابط ذرات المادة ومن ثم قدرتها على احتواء للحرارة.
السعة الحرارية
 مقالة مفصلة: سعة حرارية
مقالة مفصلة: سعة حرارية
هي كمية الحرارة اللازمة لرفع درجة حرارة كمية معينة من مادة ما درجة مئوية واحدة.
القانون الأساسي في الديناميكا الحرارية

نظام دينامي حراري : يدخل الوسط الفعال ساخنا (يسار) ويخرج (يمينا) باردا. يستخلص العمل باستخدام سلسلة من الأسطوانات.
يمكن حساب كمية الحرارة Q التي يكتسبها جسم كتلته M وارتفعت درجة حرارته مقدار dT من العلاقة :
- Q = M. C. dT
أي أن "كمية الحرارة " اللازمة لرفع درجة حرارة كتلة معينة M من المادة إلى فرق في درجة الحرارة dT ، هو حاصل ضرب الكتلة M في الحرارة النوعية C للمادة في فرق درجات الحرارة. تقاس كمية الحرارة بوحدة الجول.
مع ملاحظة أن :
كل معادلة في الفيزياء والكيمياء لا بد وان تكون متجانسة الوحدات ، بمعنى:
- كمية الحرارة M = Q كيلوجرام. C جول/(كيلوجرام.كلفن). dT كلفن
- = جول
قوانين الديناميكا الحرارية الأربعة
 مقالة مفصلة: قوانين الديناميكا الحرارية
مقالة مفصلة: قوانين الديناميكا الحرارية
القانون الصفري للديناميكا الحرارية
 مقالة مفصلة: القانون الصفري للديناميكا الحرارية
مقالة مفصلة: القانون الصفري للديناميكا الحرارية
إذا كانت حرارة الجسم أ تساوي حرارة الجسم ب وحرارة ب تساوي حرارة ج فإن حرارة أ تساوي حرارة ج.
القانون الأول للديناميكا الحرارية
 مقالة مفصلة: القانون الأول للديناميكا الحرارية
مقالة مفصلة: القانون الأول للديناميكا الحرارية
ينص على أن الطاقة في النظام تساوي العمل المبذول (المضاف أو المنتزع) يضاف إليها الطاقة الداخلية (المضافة أو المنتزعة).
أي في نظام مغلق :
- dQ= dU + dW
حيث (dQ)هي كمية الحرارة التي تخرج من أو تنتقل إلى النظام.
و(dU)هو التغير في الطاقة الداخلية للنظام (وتعتمد على درجة الحرارة) ،
و (dW) هو الشغل المبذول على أو من النظام.
توازن الطاقة في الدورات الحرارية

القانون الأول للدورة الحرارية. تمثل الدورة بنظام مغلق تدخل فيه حرارة من الخارج ، ويخرج منه شغل وحرارة غير نستفاد منها(عادم). المثال هنا يمثل عمل توربين بخاري بالحرارة الداخلة إليه (أحمر) والحرارة الخارجة منه (أزرق).
نفترض آلة مكونة من توربين غازي يدخلها البخار ساخنا ويخرج منها باردا مع اكتسابنا لشعل ميكانيكي منه. ثم نقوم بتسخين البخار من جديد لأداء دورة ثانية. يعود الوسط الفعال (البخار) إلى نقطة البداية بعد أداء دورة كاملة في الدورة الحرارية. هذا يسهل حساب الطاقة ولا نحتاج إلى حساب التغيرات في دوال الحالة للنظام ، ويبقى فقط حساب الحرارة والشغل المؤدى من النظام خلال الدورة. وسوف نري عندما نتعرض إلى القانون الثاني للديناميكا الحرارية أنه لا يمكن تحويل الطاقة الحرارية بالكامل إلى شغل (طاقة حركية أو طاقة كهربائية) ، حيث لا بد من خروج جزء من الحرارة من النظام في صورة عادم ينتشر في الوسط المحيط (الهواء مثلا).
ويمكن كتابة معادلة التوازن للدورة كالآتي حيث WKr{displaystyle W_{mathrm {Kr} }}
الشغل المكتسب من النظام :
- WKr=−∮δQ{displaystyle W_{mathrm {Kr} }=-oint delta Q}
تجمع تلك المعادلة التكامل الدائري لجميع التيارات الحرارية في الدائرة. ويكون هذا المجموع ذو إشارة موجبة إذا دخلت الحرارة من خارج النظام إليه ، وتكون أشارة المجموع سلبة الإشارة إذا خرجت الحرارة من النظام إلى الوسط المحيط. وتكون
WKr{displaystyle W_{mathrm {Kr} }} هي الشغل الذي أداه النظام (محرك مثلا أو كما هو مثالنا هنا في حالة توربين غازي) خلال دورة واحدة. ونعطي للشغل إشار سالبة عندما نكتسب من النظام شغلا(هذا ما اصطلح عليه العلماء ، أن تكون الحرارة أو الشغل الخارج من النظام ذو إشارة سالبة، ويكون ذو إشارة موجبة إذا أدينا نحن شغلا على النظام أو أمددنا النظام بحرارة من الخارج).
تكتب هذه المعادلة أيضا كدالة لمقادير الحرارة :
- WKr=Qzu−|Qab|{displaystyle W_{mathrm {Kr} }=Q_{mathrm {zu} }-left|Q_{mathrm {ab} }right|}
حيث توضح الحرارة المفقودة من النظام والتي اعطاها النظام غلى الوسط المحيط.
وبالتالي يمكننا حساب الكفاءة الحرارية للآلة :
- ηth=Qzu−|Qab|Qzu{displaystyle eta _{mathrm {th} }={frac {{Q_{mathrm {zu} }}-left|Q_{mathrm {ab} }right|}{Q_{mathrm {zu} }}}}
وتعطينا الكفاءة الحرارية لآلة ما الشغل الناتج من دورتها الحرارية ونسبتها إلى مقدار الحرارة الذي أمددنا الآلة به (وهي تكون عادة في صورة الوقود الذي تحرقة الآلة ولا بد لنا أن ندفع له ثمنا بالدولار أو الجنيهات). وأما جزء الحرارة الذي لم يتحول غلى شغل يستفاد منه فهو يخرج من النظام كعادم وينتشر في الوسط المحيط.
القانون الثاني للديناميكا الحرارية
 مقالة مفصلة: القانون الثاني للديناميكا الحرارية
مقالة مفصلة: القانون الثاني للديناميكا الحرارية
يتعلق القانون الثاني بالاعتلاج أو الأنتروبية وينص على مبدأ أساسي يقول بأن تغيرًا تلقائيًا في نظام فيزيائي لا بد وأن يترافق بازدياد في مقدار اعتلاج هذا النظام.
صاغ العالم الألماني رودولف كلاوسيوس القانون الثاني أثناء محاضرته امام الجمعية الفلسفية في زيوريخ في 24 أبريل 1865 قائلا:
" تميل الانتروبية في الكون إلى نهاية عظمى."
ويعتبر هذا النص أشهر نص للقانون الثاني. ونظرا للتعريف الواسع الذي يتضمنه هذا القانون، حيث يشمل الكون كله من دون أي تحديد لحالته، سواء كان كونا مفتوحا أو مغلقا أو معزولا لكي تنطبق عليه صيغة القانون، يتصور كثير من الناس أن الصيغة الجديدة تعني أن القانون الثاني للحرارة ينطبق على كل شيء يمكن تصوره.ولكن هذا ليس صحيحا فالصيغة الجديدة ماهي إلا تبسيط لحقيقة أعقد من ذلك.
وبمرور السنين اتخذت الصيغة الرياضية للقانون الثاني للديناميكا الحرارية في حالة نظام معزول تجري فيه تحولات معينة الشكل التالي :
- dSdt≥0{displaystyle {frac {dS}{dt}}geq 0}
حيث :
S الإنتروبي (entropy) أو الاعتلاج ،
t الزمن.
والإنتروبية هي مقياس لعدم النظام في نظام ، أي زيادة الهرجلة. والقانون يقول أن الهرجلة تسير تلقائيا وطبيعيا في اتجاه زيادة الهرجلة أو بقائها ثابتة. فمثلا إذا أذبنا قليل من ملح الطعام في كوب من الماء انتشرت جزيئات الملح وتوزعت توزيعا متساويا في الماء. هذه عملية طبيعية تسير من ذاتها ، ونقول أن انتروبية النظام قد ازدادت. إذ أن مجموع إنتروبية ملح الطعام "النقي" + إنتروبية الماء النقي يكون أصغر من إنتروبية المخلوط. أي تزداد إنتروبية النظام بأكمله (الماء النقي + الملح) بمرور الزمن بعد الخلط.
القانون الثالث للديناميكا الحرارية
 مقالة مفصلة: القانون الثالث للديناميكا الحرارية
مقالة مفصلة: القانون الثالث للديناميكا الحرارية
"من المستحيل تبريد نظام إلى درجة الصفر المطلق".
هذا القانون يحدد درجة الصفر المطلق كحد طبيعي لا يمكن تعديها إلى أقل منها. حقيقة أنه يمكن بأداء عمل كبير الاقتراب من درجة الصفر المطلقة، مثلما يحدث عند دراسة الميوعة الفائقة للهيليوم-3 حيث تصل درجته الحرجة للميوعة الفائقة عند 0.0026 كلفن ، إلا أنه من المستحيل التبريد حتى درجة الصفر.
الكمونات الدينامية الحرارية
 مقالة مفصلة: كمون دينامي حراري
مقالة مفصلة: كمون دينامي حراري
الطاقة الداخلية U(S,V,N){displaystyle U(S,V,N)} لنظام (وهي دالة للإنتروبيا S والحجم V وكمية المادة N) وجميع مشتقاتها بواسطة تحويل ليجاندر تعتبر كمونات دينامية حرارية للنظام. وتحول معادلات ليجاندر كمون الانتروبيا S{displaystyle S} بالنسبة إلى تغير درجة الحرارة T{displaystyle T} ، وكمون الحجم V{displaystyle V} بالنسبة إلى تغير الضغط ، وتغير كمية المادة N{displaystyle N} بالنسبة إلى تغير الكمون الكيميائي μ{displaystyle mu }.
تستنبط منها 3 أزواج من المتغيرات (S,T),(V,p),(N,μ){displaystyle {(S,T),(V,p),(N,mu )}} وينشأ منها بالتالي 23=8{displaystyle 2^{3}=8} كمونات ترموديناميكية.
أهم تلك الكمونات والشائعة استعمالا هي (كدوال للمتغيرات فيها) :
طاقة داخلية U=U(S,V,N){displaystyle U=U(S,V,N)}
طاقة هلمهولتز الحرة F=F(T,V,N){displaystyle F=F(T,V,N)}
إنثالبي H=H(S,p,N){displaystyle H=H(S,p,N)}
طاقة غيبس الحرة (الإنثالبي الحر) G=G(T,p,N){displaystyle G=G(T,p,N)}
كمون لانداو Ω=Ω(T,V,μ){displaystyle Omega =Omega (T,V,mu )} وهو يطبق في حالة العمليات غير العكوسية. (انظر التفاصيل في كمون دينامي حراري)
الثلاثة كمونات الباقية (ويقل استعمالها) هي :
- R=R(S,V,μ){displaystyle R=R(S,V,mu )}
- J=J(S,p,μ){displaystyle J=J(S,p,mu )}
- K=K(T,p,μ){displaystyle K=K(T,p,mu )}
العمليات الدينامية الحرارية
 مقالة مفصلة: عملية ترموديناميكية
مقالة مفصلة: عملية ترموديناميكية
العملية الترموديناميكية هي تغير نظام من حالة إلى حالة أخرى ، مثل رفع درجة حرارة النظام (غلاية مثلا). وفي حالة تواجد النظام في حالة توازن ترموديناميكي فيمكن تغير تلك الحالة عن طريق تغيير أحد دوال الحالة أو عدة منها، مثل تغيير درجة الحرارة أو تغيير الضغط والحجم وغيرها.
بدأت دراسة "عمليات التحريك الحراري " مع اختراع الآلة البخارية، ثم امتدت بعد ذلك وصاغت قوانينا تنطبق أيضا على جميع المحركات. وكذلك تنطبق قوانين الحرارة على تحول الطاقة من صورة إلى أخرى مثل تحويل طاقة الحركة إلى طاقة كهربائية (كما هو في إنتاج الكهرباء من سدود الأنهار) أو تحويل طاقة كيميائية إلى طاقة حركة كما هو مسلك محرك الاحتراق الداخلي مثلا أو تحويل طاقة كيميائية إلى طاقة كهربائية مثلما يجري في البطارية وفي خلية الوقود.
انواع عمليات الحركة الحرارية
يتغير حالة نظام حركة حرارية بتغير العديد من المتغيرات مثل درجة الحرارة , والضغط والحجم والإنتروبيا وغيرها. ولدراسة العمليات نسهل على أنفسنا فهمها بجعل أحد تلك المتغيرات ثابتا وملاحظة تغير العوامل الأخرى. من هنا نشأت بعض العمليات التي تهمنا بصفة خاصة نظرا لتطبيقاتها العملية ، وخصوصا في دراسة عمل المحركات وتحويل الطاقة إلى صور مختلفة.
وتنقسم العمليات الترموديناميكية إلى عدة أنواع :
عملية متساوية الضغط (isobaric) : وهي العمليات التي تتم تحت ضغط ثابت. مثال على ذلك التفاعلات الكيميائية التي نجريها في المختبرات ، فهي تتم تحت الضغط الجوي.
عملية متساوية الحجم (isochoric): وهي العمليات التي تتم تحت حجم ثابت.
عملية متساوية الحرارة (isothermal) :وهي العمليات التي تتم تحت درجة حرارة ثابتة ، أي نحافظ خلالها على ثبات درجة الحرارة.
عملية كظومة (adiabatic): وهي العمليات التي تتم في النظام المعزول حراريا عن الوسط المحيط به. أي نمنع خلال تلك العملية أي تبادل للحرارة بين النظام والوسط المحيط.
عملية متساوية الاعتلاج (isentropic): وهي العمليات التي تتم عند اعتلاج ثابت.
عملية متساوية الإنثالبي (isenthalpic): وهي العمليات التي تتم عند محتوى حراري ثابت.
الخصائص الحرارية
 مقالة مفصلة: قائمة الخواص الترموديناميكية
مقالة مفصلة: قائمة الخواص الترموديناميكية
من أهم الخصائص الحرارية للمواد:
الحرارة T
الضغط P
الحجم V
طاقة داخلية U
الاعتلاج (إنتروبيا) S
السخانة H (التغير في الإنثالبي يساوي التغير في الطاقة عند ثبوت الضغط لأن H=pv+U)- السرعة
- العلو
ويمكن تقسيم هذه الخصائص بطريقتين:
حالية حرارية (كدرجة الحرارة والضغط والحجم) أو حالية كالورية ، أي معبرة عن الطاقة (كالطاقة الداخلية والاعتلاج والسخانة) لجسم أو نظام ما.
حالية (أي أنها تعبر عن حالة للمادة أو حالة نظام وهي كل الخصائص المذكورة أعلاه، وتسمى دوال الحالة) ، أو عملياتية (دوال عملية ،أي أنها لا توجد إلا بوجود عملية كعملية انتقال الحرارة من جسم لآخر، وعلى ذلك فهي تمثل "تغير" حالة المادة. ومن هذه الخصائص التي تعتمد على الدوال العملية الشغل المكتسب من نظام : فقد يكون شغلا ميكانيكيا ، مثل محرك احتراق داخلي أو محرك أوتو أو آلة بخارية...وغيرها ، أو شغل كهربائي مثل البطارية وخلية الوقود وبطارية ليثيوم أيون الشائع استخدامها في هاتف المحمول.)
المعادلة الحرارية
من أهم القوانين التي تصف العلاقة بين الضغط P ودرجة الحرارة T والحجم V وعدد المولات n في غاز مثالي:
- PV =n.R.T
حيث R هو ثابت الغازات العام ولكن هذه العلاقة ليست الوحيدة وهي كذلك ليست صحيحة صحة مطلقة حيث أنه اعتمد في اشتقاقها على بعض الافتراضات المبسطة. افتراض غاز مثالي أن ذرات أو جزيئات الغاز ليس لها حجم ولا توجد قوى بين الجزيئات. كذلك افتراض أن تصادم الجزيئات يكون تصادما مرنا ، أي أن الجزيئات لا تغير شكلها عند الاصتدام.
معادلة فان دير فالس
معادلة فان دير فالس هي أيضا معادلة حرارية وهي تصف حالة غاز حقيقي حيث تأخذ حجم جسيمات الغاز (الذرات أو الجزيئات) والتآثر بينهم (من قوى جذب أو تنافر) في الحسبان :
- nRT=(p+n2aV2)(V−nb){displaystyle nRT=left(p+{frac {n^{2}a}{V^{2}}}right)left(V-nbright)}
حيث a تأخذ قوي التجاذب أو التنافر بين جسيمات الغاز في الحسبان و b تأخذ حجم وشكل الجسيمات في الحسبان.
حساب الطاقة في الترموديناميكا
تعيين توازن الطاقة من المبادئ الرئيسية في الثرموديناميكا
يحتاج تغير طور المادة - مادة صلبة إلى حالة سائلة إلى حالة غازية - وكذلك عمليات الخلط (مثل خلط الملح مع الماء ، أو خلط مواد مختلفة) يحتاج إلى "طاقة تحول " مثل حرارة انصهار ، وحرارة تبخر ، وانثالبي التسامي ، أو ما يسمى "إنثالبي التحول" ، وبالتالي فإن تلك الطاقة تتحرر خلال سير العملية في الاتجاه العكسي.
وفي حالة تغير كيميائي للمادة يمكن أن تصدر عنها "حرارة تفاعل " أو ما يسمى إنثالبي التفاعل ، أو بالعكس يمكن أن يحتاج التفاعل الكيميائي لحرارة من الخارج لكي يسير ويتم.
وبغرض حساب الحرارة الناشئة عن تفاعل كيميائي نقوم أولا بكتابة معادلة التفاعل مزودة بنسب المواد المختلفة الداخلة والخارجة من التفاعل. انثالبي قياسي للتكوين لكل مادة نقية مشتركة في التفاعل سواء الداخلة في التفاعل والناتجة من التفاعل نجدها في جداول خاصة عند 25 درجة مئوية كدرجة حرارة قياسية. ونقوم بجمع إنثالبي المواد الناتجة من التفاعل بنسبها ونطرح منها مجموع إنثالبي المواد الداخلة في التفاعل (قانون هس).
حرارة التفاعل أو " إنثالبي التحول" التي تنتج من تفاعل كيميائي أو من تحول لطور المادة وتنتشر (الحرارة الناتجة) في الوسط المحيط نعطيها إشارة سالبة. وفي حالة تزويدنا للنظام طاقة (حرارة) من الخارج لإتمام التفاعل الكيميائي أو إتمام تحول الطور (مثل تسخين الماء (طور سائل) ليتحول إلى بخار [طور غازي])، فنعطي تلك الحرارة إشارة موجبة.
يعطى الإنثالبي بالمعادلة :
- H=U+p⋅V{displaystyle mathrm { H=U+pcdot V} }
حيث:
- الإنثالبي H
- U الطاقة الداخلية
- p الضغط
- الحجم V
ويعطى الإنثالبي الحر G بالمعادلة ، وهي معروفة بطاقة جيبس الحرة:
- G=H−T⋅S{displaystyle mathrm { G=H-Tcdot S} }
حيث :
- H الإنثالبي
- T درجة الحرارة بالكلفن
- S الإنتروبيا
وبإجراء التفاضل الكامل لمعادلة الإمثالبي الحر ، ثم إجراء التكامل على المعادلة يمكن معرفة عما إذا كان التفاعل الكيميائي ممكنا (ذاتيا) أم غير ممكنا :
- ΔG=ΔH−T⋅ΔS{displaystyle mathrm { Delta G=Delta H-Tcdot Delta S} }
فإذا كان "فرق الإنثالبيات الحرة " GΔ{displaystyle Delta } لنواتج التفاعل مطروحا منها الإنثالبيات الحرة للمواد الداخلة في التفاعل ذات إشارة سالبة ، يكون التفاعل أو تحول الطور ممكنا.وعندما يكون فرق الإمثالبي الحر للتفاعل أو لتحول الطور سالبا الإشارة ، ينتج عن ذلك سير التفاعل - طالما لا يوجد ما يعطله - حتى نقطة معينة تصبح عندها
ΔG=0{displaystyle Delta G=0}.
ويعتبر
قانون فاعلية الكتلة حالة خاصة لمثل هذا التوازن ، فإذا كان الفرق في الإنثالبيات الحرة ذو إشارة موجبة ، فمعنى ذلك أن التفاعل أو تحول الطور غير ممكن.
في عام 1869 كان مارسلين بيرثولد يعتقد أن التفاعلات الكيميائية التي تنشر حرارة هي وحدها الممكنة. وشمل اعتقاده هذا أي تحول أو أي تفاعل كيميائي أنه ممكنا سواء نشر حرارة أم لم تصدر منه حرارة. وكان ذلك بأخذه في الاعتبار شق المعادلة المعبر عن تغير الإنتروبيا (T*Δ{displaystyle Delta }S).
وعلى سبيل المثال :
- عند إذابة سلفات الصوديوم في الماء تنخفض درجة حرارة المحلول عن درجة حرارة الغرفة. فيكون شق الإمنتروبيا في المعادلة ذو إشارة موجبة ، وعلي الرغم من ذلك تتزايد درجة عدم الانتظام في المحلول ، أي تزداد انتروبية النظام بذوبان السلفات.
- عند انصهار قطعة من الثلج يحتاج الثلح حرارة من الخارج لكي يتحول من طور الثلج (مادة صلبة) إلى سائل (طور السائل.
- لا ترتفع درجة حرارة الماء على الرغم من اكتساب قطعة الثلج حرارة من الجو المحيط ، وتتزايد درحة عدم الانتظام وبالتالي تتزايد إنتروبية الجزيئات في الطور السائل عنه في الطور الصلب.
- تحول الكربون في وجود ثاني أكسيد الكربون لإنتاج أول أكسيد الكربون هو تفاعل كيميائي يتميز بإنثالبية تفاعل موجبة الإشارة. وعن طريق "إنتروبية التفاعل" يمكن إزاحة توازن التفاعل (انظر توازن بودوارد) في اتجاه إنتاج أول أكسيد الكربون برفع درجة الحرارة.
أنواع تغير الحالة
 مقالة مفصلة: دورة حركة حرارية
مقالة مفصلة: دورة حركة حرارية

شكل الضغط والحجم للدورة الترموديناميكية
تحول عكوس: تحول يتم ببطء شديد ، يمكن للنظام الحراري في أي نقطة منه العودة في الاتجاه المعاكس معيداً وبدقة تامة جميع الشروط التي قد مرت به في التحول الأصلي المباشر ، ويسمى هذا التحول بالتحول الفيزيائي.
تحول لاعكوس: تحول سريع غير قابل للعكس. وتتصف جميع التحولات الطبيعية بأنها لاعكوسية؛ ويسمى هذا التحول بالتحول الكيميائي والسبب تكون ماده جديده.
الدورة المغلقة: تحول يعود فيه النظام إلى نقطة البدء بعد أن يكون قد مر بعدة مراحل مختلفة.
متغيرات مترافقة
الفكرة الأساسية في الترموديناميكا هي الطاقة. يقول القانون الأول للديناميكا الحرارية أن الطاقة الكلية في نظام والوسط المحيط بالنظام تكون ثابتة لا تتغير. فيمكن للطاقة الانتقال إلى النظام عن طريق التسخين أو زيادة الضغط ، أو زيادة كمية المادة فيه ، كذلك يمكن استخراج طاقة من النظام بالتبريد أو بالتمدد في حجم النظام أو استخراج جزء من مادته.
وفي الميكانيكا نحسب التغير في طاقة جسم كحاصل ضرب القوة المؤثرة (ق) على الجسم في المسافة (س) التي انزاحها الجسم.
والمتغيرات المترافقة في الترموديناميكا هي أزواج من المتغيرات ينتمي أحدهما إلى قوة تؤثر على نظام (ترموديناميكي) ، والمتغير المرافق يكون بمثابة "الإزاحة" الناتجة ، وجداء الإثنين يعطينا كمية الطاقة التي انتقلت إلى الجسم.
من المتغيرات المترافقة التي تهمنا في الأنظمة الترموديناميكية الثلاثة حالات الاتية:
الضغط-حجم الغاز (إحداثيات ميكانيكية);
درجة الحرارة-إنتروبية النظام (إحداثيات حرارية);
كمون كيميائي-عدد الجسيمات في النظام (إحداثيات مادية).
اقرأ أيضا
|
|
|
مراجع
↑ أبتث الترموديناميك الهندسي، 1993، د.رضوان المصري، د.ماجدة برمدا، د.نبهان خياطة، مديرية الكتب والمطبوعات الجامعية، منشورات جامعة حلب.
^ Handbuch der Experimentellen Chemie Sekundarbereich II, Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 1
^ Hans Joachim Störig: Kleine Weltgeschichte der Wissenschaften 2, Fischer Taschenbuch, Juni 1982, S. 91
^ Gerd Wedler: Lehrbuch der Physikalischen Chemie. Verlag Weinheim, 1982, S. 59
^ Lorenz: Abriß der geschichtlichen Entwickelung der Wärmelehre. In: Zeitschrift für Kälteindustrie, 1904, Heft 8, S. 144
^ H. von Helmholtz: Die Thermodynamik chemischer Vorgänge, 1882. In: Wissenschaftliche Abhandlungen von Hermann Helmholtz, Band 2. J. A. Barth, Leipzig 1882, S. 958–978
^ Handbuch der Experimentellen Chemie Sekundarbereich II, Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 11
^ Handbuch der Experimentellen Chemie Sekundarbereich II, Band 7: Chemische Energetik. Aulis Verlag Deubner, Köln, S. 9
^ Schools of thermodynamics – EoHT.info. نسخة محفوظة 07 ديسمبر 2017 على موقع واي باك مشين.
| ||||||||||||||||||||||
|
بوابة الفيزياء
بوابة الكيمياء
بوابة طاقة



































