Xrhrft

التباطؤ الزمني يفسر اختلاف ساعتين أحدهما تعرضت لتسريع في صاروخ (قمر صناعي) وأخرى على الأرض. وعلى سبيل المثال: يمر الزمن على رائد فضاء أبطأ من الزمن على الأرض بعدة ثوان. كما يأخذ عمل نظام التموضع العالمي تلك الفروق الزمنية في الحسبان طبقا لخصائص الزمكان لضبط تعيين المواقع على الأرض.

تمدد الزمن أو الإبطاء الزمني في الفيزياء (بالإنجليزية: Time dilation) عرفنا الإبطاء الزمني من النظرية النسبية الخاصة لأينشتاين حيث قام بدراسة السرعات العالية جدا جدا والقريبة من سرعة الضوء. يشاهد الإبطاء الزمني بين مشاهدين يتحركان بسرعة نسبية كبيرة جدا (نسبية لبعضهما البعض) تكون قريبة من سرعة الضوء. كما من الممكن حدوث الإبطاء الزمني عندما يكون أحدهما بالقرب من كتلة كبيرة جدا جدا (أي يكون كل منهما في مجال جاذبية مختلف عن الآخر ويكون الاختلاف كبيرا جدا جدا). مثال : مشاهد على الأرض ومشاهد على كوكب المشتري). فيمر على الواقف على الأرض وقتا أطول مما يمر على الواقف في جاذبية المشتري ، فإذا مر على الواقف على الأرض مثلا ساعة من الزمن مر على الواقف على المشتري أربعين دقيقة فقط ، ويرجع ذلك إلى شدة الجاذبية البالغة على المشتري. ولا ينشأ هذا عن تقنية الساعتين وإنما ينشأ هذا الاختلاف فقط بسبب طبيعة الزمكان كما تصفها النظرية النسبية الخاصة.

وقد ثبتت صحة نظرية أينشتاين خلال تجارب مختلفة عملية عديدة. مثل وضع ساعة في طائرة نفاثة تطير بسرعة أكبر من سرعة الصوت لمدة ساعات ثم عودتها إلى المطار. فقد وجد أن الساعة التي كانت في الطائرة توخر جزءا من الثانية بالمقارنة بالساعة الموجوة على الأرض الذي لم تتحرك.

كذلك رواد الفضاء الذين يسبحون في الفضاء بسرعات قد تبلغ 29.000 كيلومتر في الساعة، هؤلاء يمر عليهم الزمن أبطأ مما يمر على سكان الأرض، وعند عودتهم إلى الأرض يكون الرائد أصغر عمرا ممن على الأرض، وقد يبلغ هذا الفرق عدة ثوان أو أكثر كثيرا، وهذا يعتمد على سرعة تحركهم بالنسبة إلى سرعة الضوء.

الساعة الضوئية

سنستخدم لشرح الظاهرة هنا الساعة الضوئية للتسهيل.

ساعة ضوئية, إلى اليسار الساعة ساكنة , وإلى اليمين الساعة تسير بسرعة 25 % من سرعة الضوء في اتجاه اليمين.

تتكون الساعة الضوئية من مرآتين عاكستين بينهما مسافة
d {displaystyle d },
تنعكس بينهما نبضة ضوئية ، - فكّر في تلك التجربة العالمان جيلبرت لويس و ريشارد تولمان عام 1909بناءا عن نظرية أينشتاين عن النسبية.
^[1]

بالنسبة للساعة أ والتي يتحرك معها أحد فهو يشاهد أن نبضة ضوئية تنعكس بين المرآتين خلال زمن قدره T0=d/c {displaystyle T_{0}=d/c } حيث أن المسافة بينهما d وسرعة الضوء c. يسجل زمن الانعكاس عند كل مرآة ويكون الزمن الكلي 2T0 {displaystyle 2T_{0} } هو مجموع تلك الفترتين.

وعندما نحرك ساعة ضوئية ثانية ب عموديا على الخط الواصل بين المرآتين بسرعة قدرها v {displaystyle v }
فإن المشاهد الواقف بجانب الساعة أ وهو أحمد يرى أن نبضة الضوء تقطع مسافة أكبر بين المرآتين عن المسافة في ساعتة أ. وباعتبار سرعة الضوء ثابتة لا تتغير فإن أحمد يشاهد أن الساعة ب تتباطأ عن الساعة أ. وتقدر الفترة الزمنية
T′=d′/c {displaystyle T'=d'/c }, التي تقطع خلالها النبضة الضوئية المسافة d′ {displaystyle d' } بين المرآتين بالمعادلة :

d′2=d2+(vT′)2 {displaystyle d'^{2}=d^{2}+(vT')^{2} }.

وبالتعويض عن المسافتين d {displaystyle d } وd′ {displaystyle d' }
وحل المعادلة للحصول على T′ {displaystyle T' } نحصل على :

T′=T01−v2c2{displaystyle T^{'}={frac {T_{0}}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

وبالتالي

(2) T0=T′⋅1−v2c2.{displaystyle T_{0}=T^{'}cdot {sqrt {1-{frac {v^{2}}{c^{2}}}}}.}

ومن وجهة أخرى فيمكن لمشاهد بجوار الساعة ب ويتحرك بسرعتها أن يدعي - طبقا لمبدأ النسبية - أنه هو في حالة ثبات. هذا يعني أن ساعته ب انما تستغرق الزمن
2T0′ {displaystyle 2T_{0}^{'} } لحركة النبضة الضوئية ، كما يرى أن النبضة الضوئية في الساعة أ التي تتحرك بالنسبة له تقطع مسافة أكبر وتستغرق زمنا قدره :

T=T0′1−v2c2{displaystyle T={frac {T_{0}^{'}}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

وبالتالي يكون:

(1) T0′=T⋅1−v2c2.{displaystyle T_{0}^{'}=Tcdot {sqrt {1-{frac {v^{2}}{c^{2}}}}}.}.

رحلة إلى نجم بعيد

لنفترض أنّ هناك مركبة فضائية ستنطلق من الأرض لزيارة كوكب بعيد ثم ستعود إلى الأرض. ونختار أن المركبة الفضائية تتسارع بعجلة ثابتة قدرها
g=9,81ms2{displaystyle g=9{,}81,{frac {mathrm {m} }{mathrm {s} ^{2}}}}
وأن الكوكب يبعد عنا 28 سنة ضوئية (وقد اخترنا السرعة مساوية
g1{displaystyle g1} لمحاكاة ظروف جاذبية الأرض في المركبة الفضائية). بعد قطع نصف المسافة إلى الكوكب يبدأ رواد الفضاء كبح المركبة بغرض الهبوط على الكوكب وذلك بعجلة قدرها -g1{displaystyle g1} (غيرنا الإشارة بالناقص لأنها عجلة كبح).

يبقي رواد الفضاء على سطح الكوكب 6 أشهر ثم يعودون بنفس الطريقة إلى الأرض. طبقا لمعادلة تباطؤ الزمن بالنسبة للمسافر نحصل على زمن الرحلة: 13 سنة و 9 أشهر و 16 يوم (وذلك بالنسبة لساعة رواد الفضاء على متن مركبة الفضاء). وبالنسبة للأرض عند عودة مركبة الفضاء يكون زمن قدره 60 سنة و 3 أشهر و 5 ساعات قد مر.

ويمكن أن يحدث ما هو أغرب من ذلك إذا كانت الرحلة مثلا إلى أحد الكواكب في مجرة المرأة المسلسلة (مجرة) التي تبعد عنا نحو 2 مليون سنة ضوئية. فابفتراض نفس العجلة السابقة ونفس الكبح في أداء الرحلة نجد أنه عند عودة المركبة الفضائية يكون قد مرت 4 مليون سنة على الأرض بينما بالنسبة لرواد الفضاء يكون زمن قدره 56 سنة قد مرت عليهم.

• اعترض بعض العلماء على تلك النتيجة وقت صياغة أينشتاين للنظرية النسبية وقالوا أنه بالنسبة إلى راصد خارج الأرض ، على المريخ مثلا يشاهد المركبة الفضائية تخرج من الأرض وتؤدي رحلتها ثم تعود إلى الأرض. فرد عليهم أينشتاين أن ظروف المركبة الفضائية وظروف الأرض تختلفان ، إذ أن مركبة الفضاء (والرواد عليها) هم الذين عانوا عمليات التعجيل والكبح.

أي الأخوين أكبر ؟

نفترض أن أحمد عمره 31 سنة وعمر أخيه هشام 30 سنة . ونفترض أن أحمد ركب مركبة فضائية وقام بسفرية استغرقت وفق ساعته على الصاروخ سنتين فأصبح سنه 33 سنة ، في نفس الوقت يمر على هشام على الأرض 5 سنوات فيصبح سنه 35 سنة (هذا يعتمد على سرعته بالمقارنة بسرعة الضوء). فعلا يمكن أن يحدث ذلك وأكثر عندما يتحرك أحمد بسرعة مقاربة من سرعة الضوء ويظل هشام على الأرض.

تباطؤ الزمن بالجاذبية

يصف التباطؤ الزمني المتعلق بالجاذبية الاستغراق الزمني النسبي لأنظمة مختلفة (إطار مرجعي قصوري) حيث تجري على مسافات مختلفة من مركز جاذبية وتكون ثابتة بالنسبة له. مع العلم بأن تباطؤ الزمن الناتج عن الجاذبية ليس بسبب تأثير ميكانيكي على الساعات ولكنه بسبب خصائص الزمكان نفسه. فكل راصد ثابت بالنسبة إلى مركز الجاذبية يقيس الاستغراق الزمني لعملية معينة طبقا لمرجعه الزمني الخاص به الذي يتغير بتغير بعده عن مركز الجاذبية. من أحد تبعات خاصية تباطؤ الزمن الناتج عن الجاذبية ظاهرة الانزياح الأحمر الجذبوي.

الساعات والمقاييس تتراقص

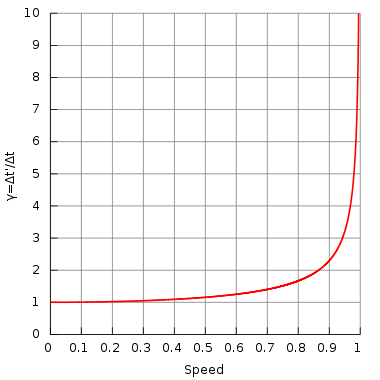
معامل لورينتز :γ≡11−v2/c2 {displaystyle gamma equiv {frac {1}{sqrt {1-v^{2}/c^{2}}}} } كدالة للسرعة (وضعنا هنا c=1)

نفترض أننا واقفون على رصيف محطة قطار نسميه "قطار أينشتاين" وتبعد عنا محطة أخرى للقطار تبعد 864.000.000
كيلومتر ، فيستغرق القطار بين المحطتين زمنا قدره ساعة حيث تبلغ سرعته 240.000 كيلومتر في الثانية. (كل تلك الأرقام أرقام بالغة الكبر ولكن يلزم هذا لتوضيح المسألة حيث أن سرعة الضوء في الفراغ تبلغ 300.000 كيلومتر في الثانية) وهي كما تقول النظرية النسبية الخاصة ثابتة في كل مكان وفي كل مختبر ولا تتغير حتى ولو كان مصدر الضوء متحركا فهي ثابت طبيعي).

يوجد في كلتا المحطتين ساعة. يركب المسافر من المحطة الأولي ويضبط ساعته قبل قيام القطار على ساعة المحطة. فيكتشف عند وصوله للمحطة الثانية تأخير ساعته بالرغم من تأكده من سلامتها قبل الرحلة.

فماذا حدث أثناء الرحلة ؟

نتصور ان المسافر يصوب نبضة ضوئية من مصباح موضوع على أرضية القطار تجاه السقف. ويوجد في السقف مرآة مثبتة تعكس نبضة الضوء القادمة إليها من المصباح. فمن وجهة نظر المسافر يرسم شعاع الضوء مسارا عموديا من أرضية القطار إلى السقف ثم يعود. نجد ان مسار النبضة الضوئية هذا يختلف تماما عن المسار الذي يشاهده الواقف خارج القطار. فأثناء سير الشعاع من المصباح إلى المرآة تتحرك المرآة متابعة لحركة القطار. ,أثناء عودة الشعاع يقطع المصباح مسافة مماثلة أخرى نظرا لحركة القطار.

أي أن شعاع الضوء يقطع بالنسبة للمشاهد خارج القطار مسافة أطول من المسافة التي يشاهدها راكب القطار. وتقول النظرية النسبية أن سرعة الضوء مطلقة (ثابتة لا تتغير فهي ثابت طبيعي) ، أي أنها متساوية لكل من الراكب والمشاهد خارج القطار. نستنتج من ذلك أن سير النبضة الضوئية من المصباح إلى المرآة والعودة يستغرق بالنسبة للمشاهد خارج القطار زمنا أطول من الزمن الذي تستغرقه النبضة الضوئية بالنسبة لراكب القطار.

ويمكننا بسهولة حساب نسبة هذا الزمن إلى ذاك.

نفرض أن المشاهد خارج القطار وجد أن مسيرة شعاع الضوء تلك قد استغرقت 10 ثوان. فخلال تلك الفترة يقطع الضوء مسافة قدرها : 300.000 * 10 = 3.000.000 كيلومتر. ينتج من المثلث أ ب ج المتساوي الضلعان أن :

أ ب = ب ج = 1.500.000 كيلومتر

ومن الواضح أن قاعدة المثلث أ ج تساوي المسافة التي قطعها القطار في 10 ثوان.

إذن:

أ ج = 240.000 * 10 = 2.400.000 كيلومتر

ومن ذلك يمكننا استنتاج ارتفاع عربة القطار والتي يمثلها لارتفاع d في الشكل أعلاه.

ونذكر انه في المثلث القائم الزاوية يتساوى مربع الضلع الأكبر (أ ب)² مع مجموع مربعي الضلعين الآخرين (أ د)² + (د ب)² ، فنجد باستخدام المعادلة :

(أ ب)² = (أ د)² + (د ب)²

بالتعويض عن تلك القيم وحساب الجذر التربيعي نحصل على ارتفاع عربة القطار :

ارتفاع عربة القطار = 9.000.000 كيلومتر

هذا ارتفاع لا شك عظيم ، ولكن لا غرابة في ذلك بالمقارنة للأبعاد العظيمة لقطار أينشتاين. وتبلغ المسافة التي يقطعها الضوء من أرضية القطار إلى سقف القطار ثم العودة ضعف هذا الارتفاع ، وذلك من وجهة نظر راكب القطار ، أي أن تلك المسافة تبلغ:

9.000.000 * 2 = 1.800.000 كيلومتر

ولقطع تلك المسافة يستغرق الضوء :

1.800.000 ÷ 300.000 = 6 ثوان

الساعات تؤخر بانتظام

بهذا تمر ي القطار 6 ثوان بينما تمضي 10 ثوان خارج القطار على المحطة. وهذا معناه أن يصل القطار المحطة في زمن قدره ساعة واحدة طبقا لساعة المحطتين بينما يكون الزمن الذي استغرقة القطار بين المحطتين :

60 دقيقة * 0.6 = 36 دقيقة فقط طبقا لساعة القطار.

أي تؤخر ساعة المسافر عن ساعة المحطة بمقدار 24 دقيقة خلال 1 ساعة.

وليس من الصعب علينا توقع ازدياد تأخير ساعة الراكب بازدياد سرعة القطار ويسفحل الأمر كلاما اقتربت سرعة القطار من سرعة الضوء. أي كلما اقترب طول الضلع (أ د) الذي يمثل مسار القطار من طول الضلع الأكبر (أ ب) الذي يمثل المسافة التي يقطعها شعاع الضوء في نفس الزمن. وبنفس ذلك القدر تقل نسبة الضلع (ب د) إلى الضلع الأكبر. تلك النسبة هي العلاقة بين الزمن داخل القطار والزمن في المحطة. فإذا اقتربت سرعة القطار من سرعة الضوء يصبح في الاستطاعة تقصير الزمن داخل القطار كيفما شئنا ، حتى إذا وصلت سرعة القطار إلى 0.9999 من سرعة الضوء ، فتمضي في القطار دقيقة واحدة بينما تمضي على المحطة ساعة كاملة.

تلك هي أحد النتائج الغريبة التي أتتبها النظرية النسبية الخاصة لأينشتاين التي صاغها عام 1905 وكان عمره 25 سنة.

عمر المسافر

يتراءى لنا أنه أصبح في الإمكان إطالة عمر الإنسان ولو من وجهة نظر الآخرين ، لأن الإنسان يكبر طبقا لساعته "الذاتية" ، فيتبين لسوء الحظ بالفحص الدقيق أن الحقيقة بعيدة عما توقعناه تماما.

فجسم الإنسان ليس معد لتحمل عجلات تفوق كثيرا عجلة جاذبية الأرض لمدة طويلة. فهو يحتاج إلى زمن طويل جدا للوصول - في صاروخ مثلا - إلى سرعة مقاربة لسرعة الضوء. وتبين التقديرات أن راكب الصاروخ يكسب 6 أسابيع خلال رحلة تستغرق 6 أشهر بعاجلة تعادل عجلة الجاذبية الأرضية. وتطول الفترة الزمنية التي يكتسبها بازدياد طول الرحلة. فخلال رحلة تستغرق سنة كاملة يكسب المرء سنة ونصف السنة. وفي رحلة تستغرق سنتين يكسب 28 سنة. فإذا ظل المسافر مسافرا بالصاروخ بعجلة مستمرة 1 g لمدة ثلاثة سنوات يكون قد مضي على الأرض 360 عاما.

الأرقام تبدو مشجعة

من وجهة نظر الطاقة اللازمة لتسريع صاروخ مستمرا بعجلة مقدارها 1 g (حيث g عجلة الجاذبية الأرضية ، وهي عجلة السقوط الحر) فلا نجد الأمر يبعث على التفاؤل. نفرض أن كتلة الصاروخ 1 طن - وهي كتلة متواضعة جدا - وسوف يسرّع من السكون إلى سرعة تبلغ 260.000 كيلومتر في الثانية في الفضاء الخارجي حيث لا تأثير لجاذبية الشمس أو الكواكب ، فعند تلك السرعة تمضي سنتان على الأرض لكل سنة على الصاروخ ، أي أنها السرعة اللازمة "لمضاعفة الزمن ". فنجد أن الطاقة اللازمة لتسريع الصاروخ تعادل الطاقة الكلية التي ينتجها العالم خلال أشهر عديدة.

كان اهتمامنا خلال تلك المناقشة تقدير الطاقة اللازمة لتسريع الصاروخ إلى نحو 0.9 من سرعة الضوء في الفضاء، ولم نأخذ في الحسبان أنه لا بد أولا من إطلاق الصاروخ خارج نطاق الأرض ، لكن هذه الطاقة تعتبر ضئيلة جدا بالمقارنة بالطاقة التي قدرناها سابق للوصول إلى تلك السرعة. فالخروج من نظاق الأرض لا يحتاج إلا جزء من الواحد في المئة من الطاقة اللازمة للتسريع المستمر ،وعلى ذلك فيمكن اهمالها. ولكن لإعادة الصاروخ إلى الأرض فلا بد من توفير الطاقة اللازمة لتهدئة سرعة الصاروخ لكي يهبط على الأرض هادئا سالما ،وهذه الطاقة تعادل بالطبع الطاقة العظيمة التي أشرنا إليها أعلاه.

الأجسام تقصر

رأينا أن الزمن قد خسر صفته المطلقة طبقا لالنظرية النسبية الخاصة وأصبح ذي خاصية نسبية ، تتطلب تعريف المختبر الذي نجري فيه القياسات. ونريد الآن توجيه اهتمامنا للمكان. وتقول النظرية النسبية أيضا أن المكان نسبي ، وقد ثبت ذلك خلال تجربة ميكلسون ومورلي التي قاما بها عام 1889 وتبعتها تجارب أخرى تثبت ذلك. وعند مناقشة "قطار أينشتاين" وتأثير السرعة على الزمن افترضنا ثبات أطوال الأجسام بصرف النظر عن المختبر الذي نشاهدها منه. وهذا ليس سليم ، إذ أن النظرية النسبية تضطرنا إلى الرجوع في هذا الرأي ، فاعتقادنا أن الأطوال مطلقة يماثل الاعتقاد بأن الزمن مطلق ، وهذا ما هو إلا وهم نشأ من اعتيادنا في حياتنا اليومية على سرعات أقل بكثير من سرعة الضوء.

نتصور مرور "قطار أينشتاين " على رصيف محطة طوله 2.400.000 كيلومتر. فهل يتفق راكب القطار معنا على هذا الطول علما بأن القطار يسير بسرعة 240.000 كيلومتر في الثانية ؟

طبقا لساعة المحطة سيقطع القطار المسافة من أول الرصيف حتى آخره في :

2.400.000 ÷ 240.000 = 10 ثوان

ولكن طبقا لساعة راكب القطار يقطع القطار المسافة في وقت أقل وقد حسبناه أعلاه بأنه 6 ثوان. من ذلك يستنتج راكب القطار أن طول رصيف المحطة :

240.000 * 6 = 1.440.000 كيلومتر وليس 2.400.000 كيلومتر.

يتضح أن رصيف المحطة يظهر أطول إذا قسناه من مختبر ساكن عن طوله إذا شاهدناه من مختبر متحرك (القطار). فكل جسم يقصر في اتجاه حركته وذلك بالنسبة للمشاهد الساكن.

لكن هذا القصر لا يدل على حركة مطلقة: إذ نحتاج فقط لوضع أنفسنا في مختبر ساكن بالنسبة للجسم فيطول ثانيا. بنفس الطريقة يظهر رصيف المحطة لراكب القطار أقصر. ويظهر "قطار اينشتاين" للواقف على رصيف المحطة أقصر (بنسبة 6 : 10) ".

هذا كله ليس خداع للنظر وأي أداة نستخدمها للقياس تعاني نفس المصير. تلك هي النتائج الغريبة التي أتت بها النظرية النسبية الخاصة وقد ثبتت عمليا خلال تجارب متعددة مختلفة قام بها الفيزيائيون خلال قرن كامل (منذ صياغة النظرية النسبية عام 1905 ، وصاغها العالم الألماني السويسري ألبرت أينشتاين).

السرعات تختل

كم تبلغ سرعة مسافر بالنسبة لقضبان السكة الحديدية إذا كان القطار يسير بسرعة 50 كيلومتر في الساعة والراكب يجري داخل القطار إلى الأمام بسرعة 5 كيلومتر في الساعة ؟ من الواضح أننا نحسب سرعة المسافر 55 كيلومتر في الساعة بالنسبة إلى قضبان السكة الحديدية. هذه النتيجة تأتي من قانون جمع السرعات ولا نريد بث الشك في صحته. ولكن عند دراستنا للنظرية النسبية تبين لنا أن هناك "حد أقصى للسرعة " في الكون (انظر زمكان) وهو يحتم محدودية التطبيق العام لقانون جمع السرعات على السرعات الكبيرة التي تقترب من سرعة الضوء. لأنه إذا افترضنا أن المسافر في "قطار أينشتاين" يتحرك بسرعة 100.000 كيلومتر في الثانية داخل القطار فلا يمكن أن تصل سرعته مثلا إلى :

240.000 + 100.000 = 340.000 كيلومتر في الثانية بالنسبة للقضبان ، لأن تلك السرعة تفوق سرعة الضوء ومثل تلك السرعة ليس لها وجود.

يتضح من ذلك أن قانون جمع السرعات الذي اعتدنا عليه في حياتنا ليس صحيحا تماما. وهو ينطبق فقط على السرعات البطيئة بالمقارنة بسرعة الضوء.

لا شك أن القارئ قد تعود تلك المتناقضات التي بينتها النظرية النسبية وأنه سوف يفهم بسهولة ضعف الإثبات الذي ذكرناه أعلاه بشأن جمع السرعات رغم وضوحه الظاهري. فقد قمنا بجمع مسافتين الأولى هي المسافة التي قطعها القطار على القضبان والمسافة الثانية التي قطعها المسافر داخل القطار. تبين النظرية النسبية أنه لا يصح جمع هاتين المسافتين ، وأن إجراء ذلك ليس سليما.

فكيف نعين سرعة راكب "قطار أينشتاين" ؟

إذا أردنا تعيين سرعة المسافر على قطار أينشتاين بالنسبة للمحطة فلا بد من تعيين المسافة التي يقطعها في ساعة واحدة طبقا لساعة المحطة وقد استخدمنا من قبل ساعة القطار لتعيين سرعة المسافر ورأينا ان السرعتين تختلفان . من تلك المشاهدات نستنتج أن جمع السرعات التي تقارب إحداها سرعة الضوء لا بد وان يتم بطريقة أخرى عما نتبعه عادة. ومن الممكن عمليا أيضاح الخلل في إجراء الجمع العادي للسرعات عندما تكون السرعات كبيرة. وفي تجربة انتشار الضوء في الماء الجاري مثلا والتي تبين أن سرعة الضوء في الماء الجاري تكون مساوية لسرعته في الماء الراكد. أي لا يصح إضافة سرعة الماء إلى سرعة الضوء لينتج سرعة أكبر من سرعة الضوء ، فقد علمنا من النظرية النسبية أن سرعة الضوء سرعة مطلقة وتحدد الحد الأقصى للسرعات.

عندما تصل إحدى السرعات إلى 300.000 كيلومتر في الثانية تتم إضافة أي سرعة إليها بطريقة أخرى. وكما نعرف لا تتغير هذه السرعة مهما تغيرت سرعة المختبر الذي نقوم فيه بالقياس. وهذا معناه أن إضافة أية سرعة إلى السرعة 300.000 كيلومتر في الثانية يعطي نفس تلك السرعة ، أي 300.000 كيلومتر في الثانية.

يمكن إيضاح النقص في قانون جمع السرعات بمقارنة بسيطة. من المعروف أن مجموع زوايا المثلث في العدسة المستوية تساوي 180 درجة. ونتخيل مثلثا مرسوما على سطح الكرة الأرضية ، فنجد أن مجموع زوايا هذا المثلث أكبر من 180 درجة ، وذلك بسبب كروة الأرض ، ويتضخم ذلك الفرق عندما تقارب مقاييس المثلث مقاييس الأرض. وكما نطبق قوانين الهندسة المستوية عند قياس مساحات صغير على الأرض ، كذلك يمكن طبيق قانون جمع السرعات على السرعات البطيئة فقط.

آلة الزمن

نفرض أن "قطار أينشتاين" لا يسير في خط مستقيم وإنما في مسار دائري بحيث يعود بعد دورة كاملة إلى النقطة التي بدأ منها الرحلة. فكما رأينا سيكتشف المسافر في القطار أن ساعته تؤخر ، ويزيد هذا التأخير بزيادة سرعة القطار. فإذا زادت سرعة قطار اينشتاين في مساره الدائري ، نصل إلى حالة تمضي فيها سنوات طويلة على ناظر المحطة في حين لا تمر على المسافر سوى ربما ساعة واحدة. فإذا عاد المسافر من رحلته (طبقا لساعته) إلى المكان الذي بدأ منه الرحلة يكتشف أن جميع أصدقائه وناظر المحطة قد توفوا بسبب كبر سنهم.

ألا يتعارض هذا مع مبدأ النسبية ؟ هل يمكننا اعتبار المسافر في حالة سكون والمحطة هي التي تقوم برحلة دائرية بنفس سرعة قطار أينشتاين؟ هذ الفرض ربما يصل بنا إلى إمكانية مرور يوم واحد على الناس في المحطة بينما تمضي على راكب القطار أعواما طويلة لكن هذا الافتراض غير سليم وتعليل ذلك كالآتي:

وضحنا من قبل أن اعتبار جسم في حالة سكون ينطبق فقط على اجسام لا تقع تحت تأثير قوى خارجية. ففي الحقيقة فإن الساعة الموجودة في قطار اينشتاين تقع تحت تأثير القوة المركزية الطاردة ، وبذلك لا يحق لنا اعتبارها في حالة سكون ففي هذه الحالة يكون الفرق الزمني بين قراءة ساعة المحطة الساكنة وقراءة الساعة الموجودة في القطار فارقا مطلقا.

من حيث المبدأ يمكننا القيام برحلة دائرية بسرعة تقارب سرعة الضوء وافتراض تحقيق "الآلة الزمنية". فنكتشف عند عوتناإلى النقطة التي بدأنا منها الرحلة بأننا قد قمنا برحلة إلى المستقبل. وفي الحقيقة يمكننا السفر بتلك الآلة إلى المستقبل فقط ولا يمكننا السفر بها إلى الماضي (بعكس ما يأتي في بعض الأفلام الخيالية المسلية).

وقد استغلت تغير الزمن بتغير السرعة في فكرة فيلم عودة إلى المستقبل (فيلم)، وكان فيلما شيقا ناجحا . ولعبت فيه سيارة ديلورين دورا هامه حيث بواسطتها كآلة زمن كان الممثل مارتي ماكفلاي والبروفيسور يتجولان بها بين الماضي والحاضر والمستقبل.

انظر أيضا

• 
  


• 
  


• 
  


• 
  


• 
  أشخاص: آرثر إيدينجتون | ألبرت آينشتاين | هيندريك لورينتز | هيرمان مينكوفسكي | بيرنارد ريمان | هنري بوانكارييه | اليكسندر ماكفارلين | هاري باتيمان | روبرت شانكلاند | بلو وييلر
  


• 
  النسبية: نظرية النسبية.

مراجع

وصلات خارجية

• Online Time Dilation Calculator


• (تستطيع هنا حساب التباطؤ الزمني).

روابط عربية (بالعربية)

• نبذ فرضية تقلص الأطوال النسبية في الإلكتروديناميك النسبي

روابط إنجليزية (بالإنجليزية)

• 
  شروح هوغ عن النسبية مقدمة جيدة عن النسبية للمستوى الجامعي.


• 
  حاسبة النسبية لعمل حسابات هندسية في المسائل النسبية كما في جمع السرع. التطبيق يتطلب جافا وقد يستغرق عدة دقائق للتحميل إذا كان الاتصال بطيئا.


• 
  السياق التاريخ للنسبية: اكتشاف النسبية الخاصة كان أمرا حتميا إذا ما أخذت الاكتشافات التي سبقته بعين الاعتبار.


• 
  لا شيء سوى النسبية فهنالك عدة طرق لاشتقاق تحويلات لورينتز من دون استخدام فرضية أينشتاين عن ثبوت الضوء. الأسلوب المتبع في هذه الورقة يعيد صياغة أسلوب معروف وبسيط.


• 
  تأملات في النسبية كتاب إلكتروني كامل عن النسبية مع قائمة مطولة بالمراجع.


• 
  محاضرات عن النسبية الخاصة عبارة عن مقدمة تقليدية لموضع النسبية الخاصة يحتوي على أمثلة توضيحية بناء على رسومات ومخططات زمكانية من جامعة فيرجينيا التقنية.


• 
  نظرية النسبية الخاصة بشكل مبسط أسلوب جديد لشرح المعنى النظري للنسبية الخاصة من وجهة نظر هندسية مبسطة.


• 
  النسبية الخاصة جامعة ستانفورد، هيلين كوين، 2003*قالب:غوتبرغ, تأليف: ألبرت أينشتاين
  


• 
  بعيني أينشتاين الجامعة الوطنية الأسترالية. تأثيرات بصرية نسبية مشروحة بواسطة الصور والأفلام.


• أساسيات كريغ إيغان


• 
  ضوء أينشتاين مقدمة غير تقنية فائزة بجائزة.


• 
  أفكار منيرة رسوم متحركة فكاهية عن النسبية الخاصة لعامة الناس، يانيك ماهي، 2005


• 
  محاكي راب للنسبية الخاصة برنامج حاسوبي يوضح تأثير السفر بسرعة قريبة من سرعة الضوء

ع ن ت نسبية نسبية خاصة خلفية مبدأ النسبية مقدمة للنسبية الخاصة النسبية الخاصة أسس حركة نسبية إطار مرجعي سرعة الضوء معادلات ماكسويل صيغة نسبية غاليلية تحويل جاليليو تحويلات لورينتز نتائج تمدد الزمن كتلة نسبية تكافؤ كتلة-طاقة تقلص الأطوال نسبية التزامن تأثير دوبلر النسبي مبادرة توماس أقراص نسبية زمكان زمكان مينكوفسكي خط العالم Spacetime diagrams مخروط ضوئي نسبية عامة خلفية مقدمة صيغة رياضية النسبية العامة مفاهيم أساسية النسبية الخاصة مبدأ التكافؤ خط العالم هندسة ريمانية Minkowski diagram ظواهر مسألة الجسمين عدسات أمواج تباطؤ الإطار المرجعي تأثير الجيوديسي أفق الحدث تفرد ثقب أسود معادلات Linearized gravity Post-Newtonian formalism معادلات أينشتاين للمجال معادلة الجيوديسي معادلات فريدمان ADM formalism BSSN formalism Hamilton–Jacobi–Einstein equation نظريات متقدمة كلوزا-كلاين جاذبية كمية نظرية برانز-ديك حلول شوارزشيلد رايسنر–نوردستروم غودل مترية كير مترية كير-نيومان كاسنر Taub–NUT ميلن روبرتسون-ووكر pp-wave van Stockum dust علماء أينشتاين لورينتز هيلبرت بوانكاريه شوارتزشيلد دي سيتر رايسنر نوردستروم فايل إدنغتون فريدمان ميلن زفيكي لومتر غودل ويلر روبرتسون باردين ووكر كير تشاندراسخار أييلرز بنروز هوكينج تيلور هالس Stockum توب نيومان ياو ثورن نوتال آخرون

ع ن ت زمن مفاهيم رئيسية ماض تاريخ زمن سحيق يوم المستقبل علم المستقبل خط زمني للمستقبل البعيد أبد جدل حول عودة أبدية خلود القياس والمعايير قياس الزمن توقيت عالمي منسق توقيت عالمي توقيت ذري عالمي وحدة زمن زمن بلانك ثانية دقيقة ساعة يوم أسبوع شهر سنة عقد قرن ألفية سنة مدارية سنة فلكية شهر قمري نظام وحدات منطقة زمنية الوقت بصيغة ال12 ساعة الوقت بصيغة ال24 ساعة توقيت صيفي توقيت شمسي وقت فلكي زمن متري زمن عشري زمن ستة عشري تقاويم تقويم ميلادي تقويم يولياني تقويم عبري تقويم شمسي تقويم هجري تقويم قمري شمسي هجري تقويم المايا إقحام ثانية كبيسة سنة كبيسة ساعات علم البنكامات تاريخ آلات قياس الوقت ساعة نموذج النظام الشمسي ساعة ذرية الكمية كرونوميتر بحري مزولة ساعة يد ساعة مائية علم التسلسل الزمني تاريخ تسلسل زمني فلكي التاريخ العظيم عصر التقويم تسلسل زمني زمن سحيق التقسيم لحقب سنة ملكية خط زمني الزمن في الدين الأساطير زمن الأحلام كالا كالاشاكرا نبوءة آلهة الزمن والقدر عجلة الزمن فلسفة الزمن سلسلة ألف وسلسلة ب نظرية بي للزمن علية مدة نظرية التحمل عودة أبدية نظرية الأبدية حدث Perdurantism الحاضرية Temporal finitism أجزاء مؤقتة عدم واقعية الزمن التجرية الإنسانية في استخدام الزمن فترة محاسبية سنة مالية قياس الزمن العقلي تسويف الدقة مدة محددة نظام زمني نظريات الوقت إدراك الزمن الحاضر الخادع برمجيات تتبع الوقت بحث استخدام الوقت عملة على أساس الزمن (زمن بنكي) قيمة وقتية للنقود ساعة زمنية ساعات العمل الزمن في جيولوجيا مقياس زمني جيولوجي عمر chron مقياس زمني جيولوجي عصر حقبة فترة علم الزمن الجيولوجي تاريخ الأرض الجيولوجي الفيزياء زمان ومكان مطلق سهم الزمن كورنون تنسيق الوقت زمن تخيلي حقبة بلانك زمن بلانك الآجال نسبة زمكان نظرية النسبية تمدد الزمن إبطاء زمني ثقالي نظاق الوقت تناظر -تي مناطق مواضيع أخرى تأريخ زمني علم الأحياء الزمني نظم يوماوي منهجيات التأريخ في علم الآثار مواضيع ذات صلة انتهز الفرصة وضعية الساعة مكان وقت النظام الوقت يطير كابسولة الزمن تعقيد الوقت شارة التوقيت سفر عبر الزمن بوابة زمن

في كومنز صور وملفات عن: تمدد الزمن

• 
  بوابة الفيزياء
  


• 
  بوابة زمن