Xrhrft

كهرومغناطيسية
كهرباء · مغناطيسية
كهربائية ساكنة
شحنة كهربائية
قانون كولوم
حقل كهربائي
تدفق كهربائي
قانون غاوس
كمون كهربائي (جهد كهربائي)
حث كهروسكوني
عزم كهربائي
مغناطيسية ساكنة
تيار كهربائي
قانون أمبير
مجال مغناطيسي
تدفق مغناطيسي
عزم مغناطيسي
قانون بيوت-سافارت
قانون غاوس للمغناطيسية
الكهرومغناطيسية التقليدية
فضاء حر
قانون قوة لورينتز
قوة دفع كهربائي
حث كهرومغناطيسي
قانون الحث لفرداي
قانون فاراداي-لينز
تيار الإزاحة
معادلات مكسويل
مجال كهرومغنطيسي
إشعاع كهرومغنطيسي
تيار دوامي
دارات كهربائية
توصيل كهربائي
مقاومة كهربائية
سعة
تحريض
معاوقة
دائرة رنين
مرشد الموجة
علماء
هاينريش رودولف هيرتس
هندريك أنتون لورنتس
جوزيف هنري
أوليفر هيفسايد
جيمس ماكسويل
تيسلا
ويليام ويبر
أندري ماري أمبير
مايكل فاراداي
شارل أوغستان دي كولوم

الحقل الكهربائي أو المجال الكهربائي في الفيزياء هو الفضاء المحيط بشحنة كهربية له خاصية تدعى الحقل الكهربي أو المجال الكهربي.^[1][2][3] هذا المجال الكهربي يؤثر بقوة على الأجسام المشحونة. قدم هذا المفهوم مايكل فاراداي.

الحقل الكهربائي في الفيزياء هو التأثير الناتج عن شحنة كهربائية (أو مجال مغناطيسي متغير) تبذل قوة على الأجسام المشحونة في المجال.

خط المجال الكهربائي

هو المسار الذي تسلُكه شحنة اختبار موجبة حرة الحركة عند وضعها في المجال, وهو خط وهمي.

خصائص خطوط المجال الكهربائي

• خطوط المجال الكهربائي خطوط وهمية اتفق على أنها تبدأ من الشحنة الموجبة وتنتهي إلى الشحنة السالبة.


• تتناسب كثافة خطوط المجال طردياً مع مقدار الشحنة الكهربائية.


• 
  تنتهي الخطوط على سطح الشحنة ولا تخترقها^{[بحاجة لدقة أكثر]}.


• يتناسب عدد خطوط المجال التي تقطع عمودية على وحدة المساحة تناسباً طرديا مع شدة المجال .


• يدل إتجاه المماس لخط المجال عند أي نقطة على إتجاه المجال الكهربائي في تلك النقطة .


• خطوط المجال الكهربائي لا تتقاطع .

خصائص خطوط المجال

شكل يوضح خطوط المجال الكهربي لشحنة موجبة (أحمر) وشحنة سالبة (أزرق).

• خطوط وهمية تخرج من الشحنة الموجبة وتدخل في السالبة.


• خطوط المجال الكهربائي لا تتقاطع.


• تدل كثافة الخطوط على قيمة شدة المجال في المنطقة حيث تتناسب طرديا معها.

المجال الكهربائي المنتظم

هو حالة خاصة من المجال ويعرف على أنه المجال الذي قيمته ثابته عند جميع النقاط ويمكن الحصول عليه من خلال صفيحتين متوازيتين مساحتهما كبيرة والمسافة بينهما صغيرة مشحونتين بنفس مقدار الشحنة لكن الأولى موجبة والثانية سالبة.

في المجال الكهربائي المنتظم تكون شدة المجال متساوية وفي نفس الاتجاه . فمثلا المجال الكهربائي بين لوحين تكون شدة المجال الكهربائي متساوية وتعادل :

E→=ΔVΔx{displaystyle {vec {E}}={frac {Delta V}{Delta x}}}

حيث :

• 
  E = شدة المجال الكهربائي ب فولت/متر،


• ΔV = فرق الجهد بالفولت
  


• Δx = المسافة بين اللوحين بالمتر.

المجال الكهربائي

هو المنطقة المحيطة بالشحنة التي تظهر منها القوة الكهربائية للشحنة.
ويرمز له بالرمز E.

شدة المجال الكهربائي

هو مقدار القوة التي تؤثر فيها الشحنة على شحنة اختبارية صغيرة موضوعه عند نقطة معينة .

الصيغة الرياضية للمجال الكهربائي

بين شدة المجال والقوة ومقدار شحنة الاختبار

الصيغة بالعربية:

حيث:-

• 
  م:- شدة المجال وتقاس "نيوتنكولوم"

كولوم :هو مقدار الشحنة التي ينقلها تيار كهربائي مقداره أمبير واحد في ثانية واحدة

• 
  ق:- القوة الكهروستاتيكية وتقاس "نيوتن"

• ش:- مقدار شحنة الاختبار وتقاس "كولوم"

الصيغة بالإنجليزية:

E=Fq{displaystyle mathbf {E} ={frac {mathbf {F} }{q}}}

حيث:

• E: شدة المجال الكهربائي ويقاس ب نيوتنكولوم
  


• F: القوة المؤثرة على الشحنة وتقاس ب نيوتن
  


• q: مقدار شحنة الاختبار وتقاس ب كولوم
  

بين شدة المجال والشحنة صاحبة المجال وبعد نقطة القياس

الصيغة بالعربية

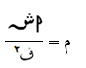
- حيث

* أ:-ثابت كولوم ويعتمد على مادة الوسط ويساوي 9×10⁹ نيوتن.م²/كولوم²

* ش:- مقدار الشحنة ويقاس "كولوم"

* ف²:-مربع المسافة بين الشحنة والنقطة المراد إيجاد المجال فيها وتقاس "م²(متر تربيع)"

وإذا أردنا أن نحسب المحصلة الكلية للمجال الناشئ عن أكثر من شحنة نقوم بدراسة المجال الناشئ عن كل شحنة على حدة ثم نقوم بتحليل تلك المجالات الناشئة متجه وثم نجمع المجالات الواقعة على كل محور. ونأتي بذلك على متجة يمثل محصلة المجالات الناشئة عن توزيع الشحنات في توزيع معين ويتم استخدام التكامل للتوزيع المتصل يكون مفيد لإيجاد المحصلة بسهولة.

المجال الكهربائي الناشئ من نقطة

يصف قانون كولوم كيف يمكن إيجاد مقدار واتجاه المجال الكهربائي الناشيء من نقطة مشحونة بالقانون التالي:

E=14πε0qr2r^ {displaystyle mathbf {E} ={1 over 4pi varepsilon _{0}}{q over r^{2}}mathbf {hat {r}} }

حيث:

q{displaystyle q} هي قيمة الشحنة الكهربائية بالكولوم.

r{displaystyle r} هي المسافة بين الشحنة الكهربائية والنقطة المراد حساب قيمة المجال الكهربائي لديها.

r^{displaystyle mathbf {hat {r}} } هو متجه الوحدة بين النقطة المشحونة والنقطة المراد حساب اتجاه المجال الكهربائي منها أو إليها.

ε0{displaystyle varepsilon _{0}}i هو الثابت الكهربائي.

وبتطبيق مبدأ التراكب يصبح حساب مقدار واتجاه المجال الكهربائي الناشئ ممكنا،حيث يجري حساب مقدار المجال الكهربائي الناشئ من كل نقطة على حدة ثم جمع كل المركبات الناتجة جمعا متجهيا ووفقا للصيغة الرياضية أدناه:

E=∑i=1nqEi=∑i=1nq14πε0qiri2r^i.{displaystyle mathbf {E} =sum _{i=1}^{n_{q}}{mathbf {E} _{i}}=sum _{i=1}^{n_{q}}{{1 over 4pi varepsilon _{0}}{q_{i} over r_{i}^{2}}mathbf {hat {r}} _{i}}.}

حيث

nq{displaystyle n_{q}} هي عدد النقاط المشحونة الكلية .

قانون غاوس الكهربائي

∇⋅E=ρε0.{displaystyle nabla cdot mathbf {E} ={frac {rho }{varepsilon _{0}}}.}

يعتمد على حساب تباعد خطوط المجال الكهربائية المتدفقة عبر سطح مغلق ويستخدم هذا القانون لحساب المجالات الكهربائية في حالات يكون فيها توزيع الشحنات الكهربائية على درجه عاليه من التماثل مثل كرات مشحونه بشحنه منتظمه التوزيع أو اسطوانات طويله أو سطوح مستويه ذات أبعاد كبيرة جدا.أما قانون كولوم فيستخم لحساب المجالات الكهربائية لشحنات كهربائيه نقطيه.

المجالات الكهربائية المتغيرة

تغير مقدار المجال الكهربائي بالنسبة للزمن يولد حتما مجالا مغناطيسيا متغيرا في الزمن،والمجال المغناطيسي المتغير يولد كذلك مجالا كهربائيا متغيرا في الزمن.،هذا أساس توليد الكهرباء والموجات الكهرومغناطيسية.و القانون الذي يحكم هذا التوليد المتناوب بين المجالين الكهربائي والمغناطيسي هو قانون فرداي الناص على ما يلي:

∇×E=−∂B∂t{displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} }{partial t}}}

where

∇×E{displaystyle nabla times mathbf {E} } تكور المجال الكهربائي.

−∂B∂t{displaystyle -{frac {partial mathbf {B} }{partial t}}} معدل تغير المجال المغناطيسي في الزمن.

طاقة المجال الكهربائي

يحمل المجال الكهربائية طاقة يبلغ قدرها

u=12ε|E|2,{displaystyle u={frac {1}{2}}varepsilon |mathbf {E} |^{2},,}

حيث u{displaystyle u} هي كثافة الطاقة الكهربائية (مقدار الطاقة الكهربائية لكل متر مكعب).ووحدة قياسها جولم³

ولحساب الطاقة الكلية يجري حساب التكامل الحجمي لكثافة الطاقة الكهربائية.

الطاقة الكهربائية الكلية =12ε∫V|E|2dV,{displaystyle {frac {1}{2}}varepsilon int _{V}|mathbf {E} |^{2},mathrm {d} V,,}

اقرأ أيضا

• شدة المجال الكهربائي


• سماحية


• سماحية الفراغ


• شحنة أولية


• قانون كولوم


• 
  نظرية الفردية .

مراجع

في كومنز صور وملفات عن: حقل كهربائي

• 
  بوابة هندسة تطبيقية
  


• 
  بوابة الفيزياء
  


• 
  بوابة كهرباء