Xrhrft

هذه المقالة عن جاذبية أرضية. لتصفح عناوين مشابهة، انظر جاذبية (توضيح).

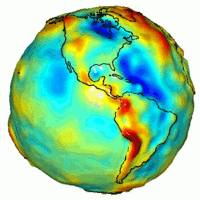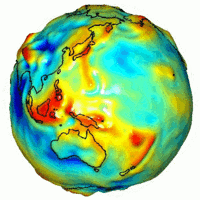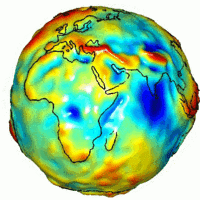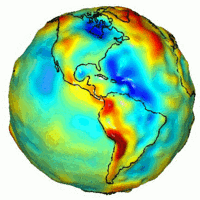
الجاذبية الأرضية بواسطة قياسات بأقمار من ناسا، توضح مدى اختلاف التوزيع الحقيقي للجاذبية عما هو مفترض نظريا لكرة متماثلة.

جاذبية الأرض أو الجاذبية الأرضية، يرمز لها في الفيزياء بـg، تشير إلى التسارع الذي تمنحه الأرض للأجسام على السطح أو بالقرب منه. يقاس هذا التسارع حسب نظام الوحدات الدولي ب‍m/s² أو مث² في بعض التراجم العربية ولها قيمة تقريبية مقدارها 9.81 m/s². معنى هذه القيمة أنه وعند إهمال تأثير الاحتكاك بالهواء أن سرعة السقوط الحر لجسم تزداد بمعدل 9.81 متر في الثانية في كل ثانية. ينبغي التفريق بين الرمز الصغير g وبين الكبير G والذي يرمز لـثابت الجذب العام.

يمكن القول أن هناك علاقة خطية تربط بين كل من وزن وكتلة الجسم، وبين تسارع الثقالة هذا ولذا قد يعبر عن الوزن بدلالة الكتلة تحت اسم مماثل يدعى قوة ثقالة. مع ذلك قد يتأثر هذا الوزن مع دوران الأرض حول نفسها بسبب تغير صافي التسارع الناجم عن كل من الجاذبية والطرد المركزي.

تعطى القيمة الدقيقة لقيمة الجاذبية الأرضية من تعريف الجاذبية القياسية وهي 9.80665 m/s² كما أنها ليست القيمة الموجودة على خط الاستواء والتي تساوي 9.78033 m/s².

تباين الجاذبية والجاذبية الظاهرية

يمكن تصور قوة الثقالة على أنها كرة عطالية ذات كثافة منتظمة. مثل هذا الجسم يمكن أن يولد حقلا متماثلا في القيمة والاتجاه على جميع النقاط على سطحه. في الواقع هناك بعض الاختلاف الضعيف في كل من القيمة والاتجاه عبر السطح وذلك بسبب عدم تماثل أيا من الكميتين المفترضتين تماما.

إضافة لذلك، فإن القوة المبذولة على الجسم بسبب تغير ما يدعى الجاذبية الظاهرية أو الجاذبية الفعالة وذلك لوجود قوى أخرى. تتغير شدة الثقالة الأرضية بتغير كل من خط العرض، العلو وطبيعة الأرض الطوبوغرافية والجيولوجية.

خط العرض

تباينات الجاذبية الأرضية حول القارة القطبية.

معلوم أن جاذبية الأرض أضعف بالقرب من خط الاستواء وذلك بسبب دوران الأرض الذي يولد قوى طرد مركزية.
تولد الأرض قوى جذب مركزية، عاملة على حفظ الأجسام على سطحها (بما في ذلك حفظ السطح نفسه) بحيث تدور معها. يمكننا تخيل ما سيحدث لو أن الأرض توقفت فجأة عن الدوران، فسوف تتطاير الكائنات باتجاه حركتها وفقا لقوانين نيوتن للحركة (هنا التوقف عن الحرك وعواقبه يعتمد على نوع التوقف. إذا كان التوقف هو عن الدوران المغزلي فقط فسوف تتطاير الأجسام نحو الأمام بسرعات تعتمد على دوائر العرض أما عند توقف الأرض عن الدوران حول الشمس فسوف تتطاير الأجسام نحو الفضاء الخارجي بسرعة واحدة تقريبا هي سرعة دوران الأرض حول الشمس).
بالمثل فإننا نتوقع أن دوران الأرض حول نفسها وبالتالي دوران الأجسام معها بنفس الكيفية سوف يولد قوى طرد مركزية تعاكس قوى الجاذبية. تزداد قوى الطرد هذه عند خط الاستواء وتقل عند الأقطاب وذلك نتيجة لتغير نصف القطر الدوراني الفعال. يمكن معرفة تفاصيل هذه العلاقة في الأسفل (انظر قسم نماذج رياضياتية).

العلو

حقل الجاذبية في الأرض

نعلم أن الجاذبية الأرضية تكاد تتلاشى في الفضاء الخارجي وهذا يعني أنها تتناقص كلما ابتعدنا عن سطح الأرض.
تستعمل العلاقة التقريبية التالية لحساب مدى تغير الجاذبية بالعلو:

gh=g0(rere+h)2{displaystyle g_{h}=g_{0}({frac {r_{e}}{r_{e}+h}})^{2}}

حيث

• 
  gh{displaystyle g_{h},} الجاذبية مقاسة على ارتفاع h{displaystyle h,} فوق سطح البحر.


• 
  re{displaystyle r_{e},} نصف قطر الأرض.


• 
  g0{displaystyle g_{0},} الجاذبية القياسية.

الطوبوغرافيا والجيولوجيا

تتسبب التغيرات المحلية في الطوبوغرافيا (وجود الجبال مثلا) والجيولوجيا (مثل كثافة الصخور القريبة) في تقلبات في الحقل الثقالي، المعروف بشذوذ الجاذبية . بعض هذا الشذوذ يمكن أن يكون واسع الانتشار، متسببا بنتوءات في مستوى البحر وتخرج بالساعات البندولية عن مجال التزامن.

مقارنات الجاذبية في مناطق مختلفة من العالم

نماذج رياضية

يمكن تقدير قيمة على سطح البحر بالعلاقة g:

gϕ=9.78031846(1+0.0053024sin2⁡ϕ−0.0000058sin2⁡2ϕ) m/s2{displaystyle g_{phi }=9.78031846left(1+0.0053024sin ^{2}phi -0.0000058sin ^{2}2phi right) m/s^{2}}

حيث

 gϕ{displaystyle g_{phi }} = التسارع بوحدات m·s⁻² على خط عرض : ϕ{displaystyle phi }

وهذه هي الصيغة القياسية 1967, معادلة هيلمرت أو صيغة كليرولت.^[1]

التصحيح الأولي لهذه الصيغة هو تصحيح الخلو من الهواء (FAC), والذي يضع في الحسبان الارتفاعات فوق سطح البحر. تقل الجاذبية مع العلو بمعدل أشبه مايكون خطيا بالقرب من سط الأرض بحيث يعطي تقاطعا صفري الجاذبية عند ارتفاع مقداره نصف قطر الكرة الأرضية أو حوالي9.8 m·s⁻² لكل 3 200 km. بالتالي:

gϕ=[9.780327(1+0.0053024sin2⁡ϕ−0.0000058sin2⁡2ϕ)−3.086×10−6h] m/s2{displaystyle g_{phi }=left[9.780327left(1+0.0053024sin ^{2}phi -0.0000058sin ^{2}2phi right)-3.086times 10^{-6}hright] m/s^{2}}

حيث

h = الارتفاع بالأمتار فوق سطح البحر

بالنسبة لمنطقة فوق مستوى سطح البحر فإن حداً آخر يتم إضافته للمعادلة نتيجة للكتلة الإضافية. لهذا الغرض يمكن تقريب الكتلة الإضافية بشريحة أفقية لانهائية ومن ثم نحصل 2πG مضروبة بالكتلة لوحدة المساحات, أي 4.2×10⁻¹⁰ m³·s⁻²·kg⁻¹ (0.042 μGal·kg⁻¹·m²)) (تصحيح بوغر). من أجل متوسط كثافة صخور 2.67 g·cm⁻³ هذا يعطي 1.1×10⁻⁶ s⁻² (0.11 mGal·m⁻¹). بدمج هذا مع تصحي الخلو من الهواء هذا يعني نقص في الجاذبية على السطح بـca. 2 µm·s⁻² (0.20 mGal) لكل متر من الصعود على المنطقة. (يلتغي كلا التأثيرين على سطح كثافة صخرية مقدارها 4/3 مرة من متوسط الكثافة الكلية للأرض.)

يمكن كتابة معادلة هيلميرت بطريقة مكافئة للصيغة السابقة إما على الصورة:

 gϕ=(9.8061999−0.0259296cos⁡(2ϕ)+0.0000567cos2⁡(2ϕ)) m/s2{displaystyle g_{phi }=left(9.8061999-0.0259296cos(2phi )+0.0000567cos ^{2}(2phi )right) m/s^{2}}

أو بالصورة

 gϕ=(9.780327+0.0516323sin2⁡(ϕ)+0.0002269sin4⁡(ϕ)) m/s2{displaystyle g_{phi }=left(9.780327+0.0516323sin ^{2}(phi )+0.0002269sin ^{4}(phi )right) m/s^{2}}

هناك صيغة أخرى بديلة لـ g بدلالة خط العرض WGS (النظام الجيوديسي العالمي) 84 صيغة الثقالة البيضوية:

 gϕ=(9.7803267714 1+0.00193185138639sin2⁡ϕ1−0.00669437999013sin2⁡ϕ) m/s2{displaystyle g_{phi }=left(9.7803267714~{frac {1+0.00193185138639sin ^{2}phi }{sqrt {1-0.00669437999013sin ^{2}phi }}}right) m/s^{2}}

المصادر

اقرأ أيضا

• قياس الثقالة


• الجاذبية


• جدس


• قطار الجاذبية


• جاذبية اصطناعية

في كومنز صور وملفات عن: جاذبية أرضية

• 
  بوابة الفضاء
  


• 
  بوابة علم الفلك
  


• 
  بوابة الفيزياء
  


• 
  بوابة علوم الأرض