إسقاط مساو للقياس
الإسقاط المساوي للقياس (Isometric projection) هو نوع من أنواع الاكسنومتري العمودية.[1][2] تستخدم, ككل أنواع الاكسنومتري, لتمثيل الأجسام ثلاثية الأبعاد على نفس المستوى. في هذا النوع من الاكسنومتري, إذا أخذت 3 مقاسات متساوية ومنتمية إلى المحاور الثلاثة xyz، فان صورتها بعد الإسقاط تقل بنفس المقياس, أي ان هناك تساوي بين وحدات القياس Ux=Uy=Uz. السبب لذلك ان الزاويات التي تشكلها المحاور بالتوالي مع مستوى الإسقاط تكون متساوية.
والجدير بالعلم ان كل محور يقطع مستوى الإسقاط في نقطة تسمى اثر المحور, مثلاً نقطة تقاطع المحور x مع مستوى الإسقاط تسمى اثر x ويرمز لها, Tx، لذلك, في الاكسنومتري الايزومترية, المثلث الذي يتكون من أثار المحاور الثلاث Tx Ty Tz يكون مثلث متساوي الأضلاع ويسمى مثلث الاثار.
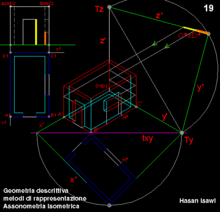
تمثيل ايزوميتري (أو متساوي القياس) لبيئة متوازية السطوح
هذا المثلث, في النوعين الاخريين من الاكسنومتري العمودية, يكون:
- متساوي الضلعين في الاكسنومتري الديمترية
- مختلف الأضلاع في الاكسنومتري التريمترية
مراجع
^ Ingrid Carlbom؛ Joseph Paciorek؛ Dan Lim (December 1978). "Planar Geometric Projections and Viewing Transformations". ACM Computing Surveys. ACM. 10 (4): 465–502. doi:10.1145/356744.356750. .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ A Chinese perspective for cyberspace?". In: International Institute for Asian Studies Newsletter, 9, Summer 1996. نسخة محفوظة 05 فبراير 2016 على موقع واي باك مشين.
بوابة هندسة رياضية